5.2. 【例題】KdV方程式¶

5.2.1. 方程式 ¶

以下の非線型偏微分方程式はKorteweg-de Vries (KdV)方程式と呼ばれます：

(1)¶ $\frac{\partial u(x,t)}{\partial t} + 6 u(x,t) \frac{\partial u(x,t)}{\partial x} + \frac{\partial^3 u(x,t)}{\partial x^3} = 0$

$u(x,t)$ は実数とします。各項の係数や符号は変数変換で変わるので、重要ではありません。慣例的に第2項の係数を6とする文献が多いので、ここではそれに従っています。この方程式は 孤立波 （ソリトン と呼ばれる）を解として持つことが知られています。この方程式を数値計算によって解いて、孤立波を確認してみましょう。

方程式の解説 ¶

KdV方程式を含む非線形方程式については文献 [4] をお勧めします。以下はその概要です（かなり大雑把ですが）。

KdV方程式は水深の浅い水面を進む波（浅水波）を記述する方程式として、1895年にKortewegとde Vriesによって定式化されました。(1) 式の第2項（非線形項）は波の上部ほど速度が速くなって波形が前のめりになる効果（波の突っ立ち）を表します。第3項は波を広げる役割があり、分散項と呼ばれます。非線形項の波形を崩す効果と分散項の波形を広げる効果がうまくつり合って、KdV方程式は非線形方程式であるにもかかわらず、波形の形を保ったまま進む進行波を解として持ちます。

KdV方程式は非線型方程式なので、解の重ね合わせが成り立ちません。しかし、2つの進行波が衝突して互いに離れた後、それぞれの波形を保ちます。このように、この進行波は粒子的な振る舞いをすることから、solitary waveまたはsolitonと呼ばれます。

KdV方程式は1950年代以降のフェルミ・パスタ・ウラムの問題 (FPU問題) に関連した研究で脚光を浴びました。フェルミらは、統計力学におけるエルゴード性の検証のために、非線形性を考慮した連成振動模型を考えました。通常の（線形の）連成振動の場合、各振動モードが独立に運動するため、そのエネルギーは保存されますが、非線型性を考慮した場合にはモード間に結合が生じ、モード間でエネルギーのやり取りが起こります。そのため、充分時間が経てば、初期状態に依らず、全てのモードに等しくエネルギーが分配された平衡状態に達する（熱化する）と予想できます。しかし、数値計算の結果、平衡状態への熱化は起きず、一定時間後に初期状態に戻る 再起現象 が観測されました。この現象は、非線形方程式における孤立波の存在を示唆します。実は、FPU問題の非線形連成振動模型は、ある極限でKdV方程式に一致し、KdV方程式と同じ孤立波を解として持ちます [4]。

数値解法 ¶

偏微分方程式の解法に従って、空間座標 $x$ を離散化し、 $u(x,t)$ を $\bm{u}(t) \equiv (u(x_0,t), u(x_1,t), u(x_2,t), \cdots)^\mathrm{T}$ とベクトル表示します（ $T$ は転置）。すると、方程式 (1) は

(2)¶ $\frac{d \bm{u}(t)}{dt} = -6 \bm{u}(t) \circ D_{x} \bm{u}(t) - D_{xxx} \bm{u}(t)$

と表されます。ここで、 $\circ$ はベクトルの成分同士の掛け算を表す記号（アダマール積）です。 $D_{x}$ と $D_{xxx}$ は微分演算子の行列表現です。2次精度の差分公式を用いた場合の $D_{x}$ の具体的な表現は差分にあります。同様に、 $D_{xxx}$ にも2次精度の差分公式を適用すると、その具体的な表現は

$D_{xxx} = \frac{1}{2h^3} \begin{pmatrix} 0 & -2 & 1 & 0 & \cdots & 0 & -1 & 2 \\ 2 & 0 & -2 & 1 & \ddots & & 0 & -1\\ -1 & 2 & 0 & -2 & \ddots & \ddots & & 0 \\ 0 & -1 & 2 & 0 & \ddots & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & 0 \\ 0 & & \ddots & \ddots & \ddots & \ddots & \ddots & 1 \\ 1 & 0 & & \ddots & \ddots & \ddots & \ddots & -2 \\ -2 & 1 & 0 & \cdots & 0 & -1 & 2 & 0 \end{pmatrix}$

となります。詳細は差分を参照してください。方程式 (2) は変数 $t$ に関する常微分方程式なので、常微分方程式の解法を使って解くことができます。

5.2.2. 実装 ¶

ソースコード kdv_solve_ivp.py

常微分方程式を解くには scipy.integrate.solve_ivp を使います。常微分方程式の例（【例題】ロジスティック方程式）では、1変数の場合の使用例を示しましたが、使い方は全く同じです（実際、1変数を1成分ベクトルとみなしてsolve_ivp関数を使いました）。

注釈

以前のドキュメントでは、SciPyを使わずにルンゲ・クッタ法を自作して実装していました。古いドキュメントはこちらです。

まずは差分を表す行列 $D_x$ と $D_{xxx}$ を作ります。この部分は他の例題でも使用するので、別ファイルとして関数を定義します。

ソースコード differential.py

import numpy as np
from scipy.sparse import csr_matrix as sparse_matrix

# scipy.sparse.csr_matrix
# https://docs.scipy.org/doc/scipy/reference/generated/scipy.sparse.csr_matrix.html


def make_differential_ops(nx, dx):

    # operators (matrix) that shift vector components (periodic boundary condition)
    f0 = np.identity(nx, dtype=int)  # f_{i}
    f1 = np.roll(f0, 1, axis=1)  # f_{i+1}
    f2 = np.roll(f0, 2, axis=1)  # f_{i+2}
    f_1 = f1.transpose()  # f_{i-1}
    f_2 = f2.transpose()  # f_{i-2}

    # (f_{i+1} - f_{i-1}) / (2 dx)
    deriv1 = sparse_matrix(f1 - f_1) / (2.0 * dx)

    # (f_{i+1} - 2f_{i} + f_{i-1}) / (dx^2)
    deriv2 = sparse_matrix(f1 - 2.0 * f0 + f_1) / dx**2

    # (f_{i+2} - 2f_{i+1} + 2f_{i-1} - f_{i-2}) / (2 dx^3)
    deriv3 = sparse_matrix(f2 - 2.0 * f1 + 2.0 * f_1 - f_2) / (2.0 * dx**3)

    return deriv1, deriv2, deriv3

2階微分は今回は使用しませんが、ついでに実装しています。この関数は最初に1度呼び出すだけなので、計算時間にはほとんど影響しません。

今回作る行列は規則的なものなので、単位行列（numpy.identity で生成）から基本的な操作を組み合わせることで、for文を使わずに書けます。ここではまず、 numpy.roll を使って単位行列を右方向(axis=1 で指定)に1つまたは2つずらした行列（f1 および f2）を作っています。このとき右にはみ出した要素は左に戻ります。これは周期境界条件に対応しています。

最終的に得られる行列は疎行列なので scipy.sparse モジュールを利用します。疎行列クラスとしていくつか選択肢がありますが、ここでは scipy.sparse.csr_matrix (Compressed Sparse Row format)を使用しています。右からベクトルを書ける演算が中心なので、行列を行ベクトルとして持っていた方が若干効率がよさそうという理由です（大差はないと思います）。

make_differential_ops で作った行列（df1, df3 とします）を使うと、空間微分を差分で置き換えたKdV方程式 (2) の右辺は以下のようにシンプルに書けます：

def f_kdv(t, u, df1, df3):
    u_x = df1.dot(u)
    u_xxx = df3.dot(u)
    return -6.0 * u * u_x - u_xxx

この関数はベクトル $\bm{u}(t)$ を受け取って、ベクトル $d\bm{u}(t)/dt$ を返します。引数 t は関数内で使用しませんが、ソルバーの仕様に合わせるために必要です。その他の引数 df1 と df3 は (2) 式右辺の計算に必要なので、パラメーターとして関数に与えます。

次に、main関数を見ていきます。まず、x座標を離散化したメッシュを作成します。

def main():
    # x mesh
    nx = 1000
    x_max = 100.0
    x = np.linspace(0, x_max, nx, endpoint=False)
    dx = x[1] - x[0]
    print("dx =", dx)

メッシュの作成には numpy.linspace 関数を使うと便利です。endpoint=False は最後の点 x_max を含めないという意味です。つまり、作られる配列は x[0]=0, x[1]=x_max/nx, ..., x[nx-1]=x_max/nx*(nx-1) となります。周期境界条件から $u(x_\mathrm{max}, t)=u(0, t)$ なので、 $x=x_\mathrm{max}$ を除いています。

ここでは、初期条件を $u(x, 0)=\sin(2\pi x/x_\mathrm{max})$ とします。

    # initial condition
    u0 = np.sin(x * (2.0 * np.pi / x_max))

numpy.sin 関数に与える引数 x が1次元配列なので、u0 にも同じ大きさの1次元配列が入ります。

注釈

NumPyの多くの関数は、引数に配列を与えると、配列の各成分ごとに関数を実行して結果を配列として返してくれます。公式ドキュメントで、第一引数と戻り値の説明に array_like と書かれていたら配列に対応しています（例えば、numpy.sin）。これを、関数が ベクトル化 されていると言います。自作の関数をベクトル化するには numpy.vectorize 関数を使います。

あとはこの関数を scipy.integrate.solve_ivp 関数に渡せば時間発展が計算されます。

    # differential operators
    op_df1, _, op_df3 = make_differential_ops(nx, dx)

    print("Solving equation...")
    t_max = 10.0
    sol = solve_ivp(f_kdv, (0, t_max), u0, dense_output=True, args=(op_df1, op_df3), rtol=1e-8)
    print(sol.message)
    print(" Number of time steps :", sol.t.size)
    print(" Minimam time step    :", min(np.diff(sol.t)))
    print(" Maximum time step    :", max(np.diff(sol.t)))

28行目：左辺のアンダーバー '_' は、関数の戻り値を破棄するという意味です。2階微分は使用しないので2番目の戻り値を捨てています。32行目：scipy.integrate.solve_ivp 関数を呼び出して時間発展を計算します。最後の引数 rtol=1e-8 で相対誤差を指定して、精度を上げています。この例題の場合、デフォルトの精度では十分ではありません（失敗例も最後に示します）。34～36行目：ソルバーが適応刻み幅制御に対応しているので、時間発展のステップ数や刻み幅の最大値・最小値を表示しておきます。

注釈

KdV方程式は不安定性が現れやすいので、本来なら、陰解法（method='Radau' や 'BDF'）を使用するのが妥当です。しかし、陰解法は陽解法に比べて計算時間がかかるので、ここでは陽解法を使用しました。陽解法でも精度を挙げれば不安定性を回避でき、陰解法よりも計算時間が短くて済みます。

解いた後で、アニメーション作成用のデータを取得します。

    # t mesh
    nt = 101
    t = np.linspace(0, t_max, nt)
    dt = t[1] - t[0]
    print("dt =", dt)

    # get u(t, x)
    u_xt = sol.sol(t)  # u(x, t)
    u_tx = u_xt.T  # u(t, x)
    print("shape of u(t, x) :", u_tx.shape)

40行目：アニメーションで表示する時刻tの等間隔メッシュを作ります。45行目：各時刻上での関数 $u(x, t)$ を計算し、2次元配列として受け取ります。46行目：2次元配列 $u(x, t)$ を $u(t, x)$ に変換します（アニメーションを作成する関数の仕様に合わせるため）。

データをファイルに保存します。今回の計算は一瞬では終わらないので、データを一旦ファイルに保存しておいて、グラフ作成は別のスクリプトで行います。こうして計算とグラフ作成を切り離しておけば、グラフの調整を簡単に行うことができます。

    # Save results
    np.savez("kdv_solve_ivp", x=x, t=t, u_tx=u_tx)

NumPy配列のデータを保存するには、numpy.savez 関数を使います。第1引数で出力するファイル名を指定します。実際に出力されるファイル名は、この文字列に拡張子".npz"が付いたものです（この場合は"kdv_solve_ivp.npz"）。第2引数以降に、保存したいNumPy配列を key=変数名 の形式で与えます。keyは任意の文字列です。データをファイルから取り出す際に、ここで指定したkeyを使います。

なお、NumPy配列を一つだけ保存する場合には、numpy.savez 関数の代わりに numpy.save 関数を使うこともできます。詳細はリンク先の公式ドキュメントを参照してください。

5.2.3. 実行結果 ¶

dx = 0.1
Solving equation...
The solver successfully reached the end of the integration interval.
Number of time steps : 24471
Minimam time step    : 0.0002880236208611109
Maximum time step    : 0.03763835219541923
dt = 0.1
shape of u(t, x) : (101, 1000)

手元のパソコンでは15秒ほどかかりました。時間のステップ数は約2.5万回、刻み幅は $10^{-4}$ から $10^{-2}$ と2桁の範囲で変化していることが分かります。実行したディレクトリに、kdv_solve_ivp.npzという名前のファイルが出力されているはずです。

5.2.4. アニメーション ¶

スクリプト ¶

ソースコード kdv_anim_artist.py

保存したデータを読み込んで、アニメーションを作成します。データをファイルから読み込む部分から見ていきます。

def main():
    # Load results
    npz = np.load("kdv_solve_ivp.npz")
    print("npz.files =", npz.files)

    x = npz['x']
    t = npz['t']
    u_tx = npz['u_tx']
    print("x.shape =", x.shape)
    print("t.shape =", t.shape)
    print("u_tx.shape =", u_tx.shape)

    # make an animation
    print("Making animation...")
    save_animation(x, t, u_tx, ymin=-1.5, ymax=3.0, filename="kdv_solve_ivp.gif")

numpy.savez 関数で保存したデータは numpy.load 関数で読み込みます。load関数の引数にファイル名を与えます。この際、savez関数の場合と異なり、拡張子を含んだファイル名を指定する必要があるので注意が必要です。各NumPy配列にアクセスするには、保存時に指定したkeyを使って、辞書型変数の形式で記述します。

アニメーションを作成する部分は関数としてまとめておきます。

def save_animation(x, t, u_tx, ymin, ymax, filename):
    fig, ax = plt.subplots()

    # common setting for plot
    ax.set_xlabel("$x$")
    ax.set_ylabel("$u(x)$")
    ax.set_ylim((ymin, ymax))

    artists = []  # list of plot
    for i in range(t.size):
        # Make i-th plot
        # ax.set_title("t = %f" % t[i])
        artist = ax.plot(x, u_tx[i, :], '-b')
        artist += [ax.text(0.05, 1.05, "t = %.2f" % t[i], transform=ax.transAxes)]
        artists.append(artist)

    # Make animation
    anim = animation.ArtistAnimation(fig, artists, interval=100, repeat=False)
    # plt.show()

    # Save animation
    anim.save(filename, writer="pillow")  # writer="pillow" or "imagemagick" for GIF
    print("saved as '{}'".format(filename))

アニメーション作成にはMatplotlibの matplotlib.animation モジュールに含まれるFuncAnimationクラスまたはArtistAnimationクラスを使います。これらの違いは、FuncAnimationはMatplotlibの関数型インターフェースを使用してグラフ描画し、ArtistAnimationはオブジェクト指向インターフェースを使用してグラフ描画をします。ここではArtistAnimationを使用します（参考のため、FuncAnimationを使用した場合の例も置いておきます）。

ArtistAnimation関数を使用する場合には、アニメーションに使用するグラフを一旦全て作成してリスト形式（各要素が動画の1フレームに表示するグラフ）で持っておきし、そのリストから動画を作成します。

12行目：オブジェクト指向インターフェースでグラフを作成するために、subplots()関数を使ってFigureオブジェクトとAxesオブジェクトを生成します。15～17行目：ラベルや軸の範囲などを設定します。19行目：アニメーションに使用するグラフを保持するためのリストを生成します。20行目：時刻tに関するforループを回し、このブロック内でグラフを作成します。23行目：ax.plot() でグラフを作成し、その戻り値をartist変数に格納します。artistはグラフの構成要素（Artistと呼ぶ）をリスト形式で持っています。24行目：ax.text() で時刻tの値をテキストとして描画し、その戻り値を先ほど取得したリストartistに追加します。ax.text() を [] で囲んでいるのは、ax.text() の戻り値を要素数1のリストにするためです（ax.plot() の戻り値は複数のArtistのリスト、ax.text() の戻り値はひとつのArtist（リストではない）という違いがあります）。25行目：artistをartistsに追加します。

28行目：以上により作成した全てのグラフ（artistsリストが保持）を、ArtistAnimation関数に渡してアニメーションを作成します。interval は1フレームごとの時間（ミリ秒）です。interval を大きくするとアニメーションが遅くなります。その他にもパラメータがありますが、詳細は公式ドキュメント matplotlib.animation.ArtistAnimation を参照してください。

32行目：アニメーションをファイルに保存します。GIFアニメーションの場合は writer 引数に "pillow" または "imagemagick" を指定します。後者を利用するにはImageMagickライブラリのインストールが必要です。writerクラスの詳細については、matplotlib.animation#Writer-Classes を参照してください。Jupyter Notebookなどの画面上でアニメーションを表示したい場合には、29行目の plot.show() を実行します。

結果 ¶

npz.files = ['x', 't', 'u_tx']
x.shape = (1000,)
t.shape = (101,)
u_tx.shape = (101, 1000)
Making animation...
saved as 'kdv_solve_ivp.gif'

下図は出力されたgifアニメーションです。

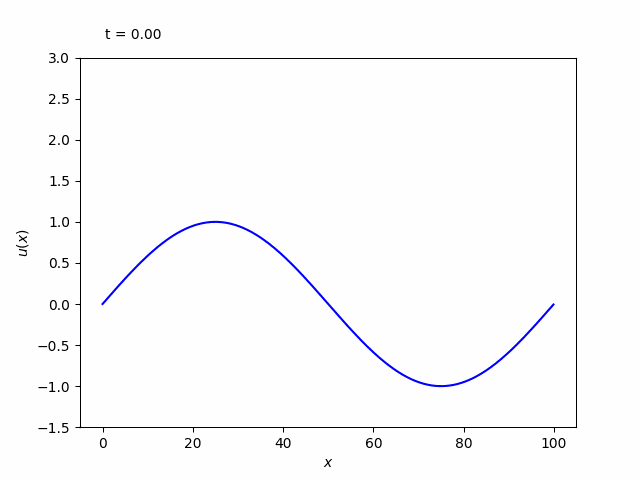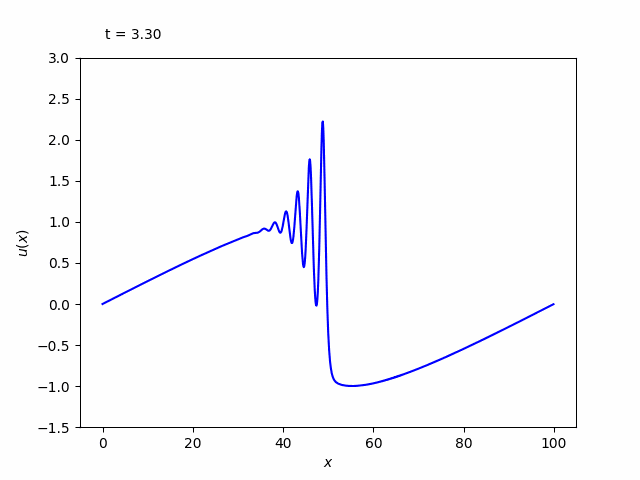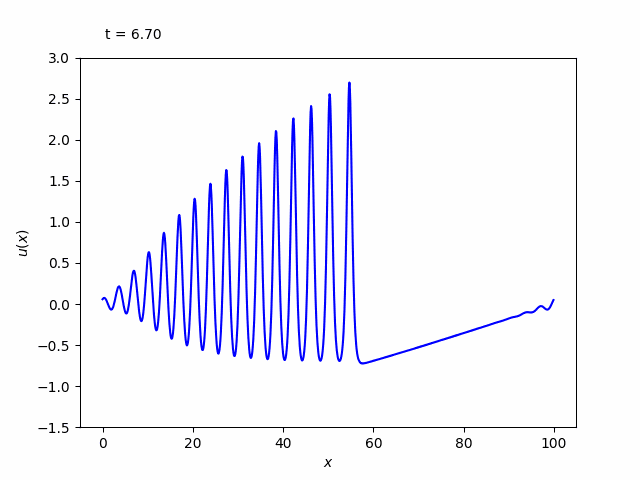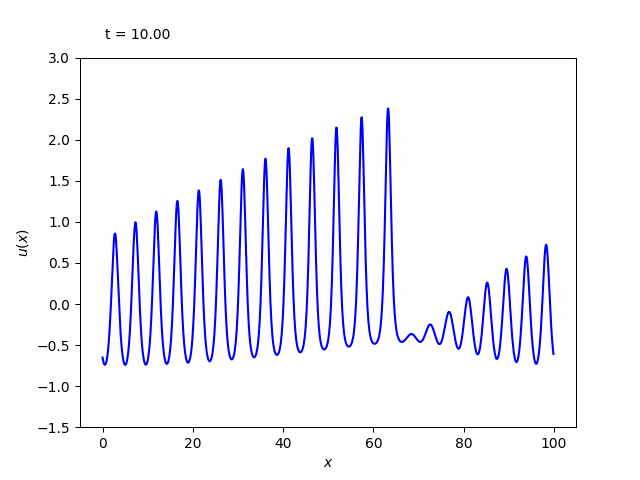
いくつものピークに分かれて、個別に進行していく様子が分かります。これをソリトンと呼びます。

注釈

ソリトンは、互いに衝突した後もその波形を保ちます。このように粒子のように振る舞うことから、solitary（孤立）に粒子を表す-onを付けて、solitonと名づけられました。ぜひ、1ソリトン解や2ソリトン解を初期条件として時間発展を観察し、ソリトンの性質を調べてみてください。

5.2.5. 失敗例 ¶

KdV方程式は3階微分を含むので、時間発展の計算が非常に不安定です。 $\Delta t$ を十分小さく、具体的には

$\frac{\Delta t}{\Delta x^3} \lesssim 1$

を満たすようにしないといけません（偏微分方程式の解法を参照）。上の例では、 $\Delta x=10^{-1}$ なので、 $\Delta t \lesssim 10^{-3}$ が目安です。

上の例で使用しているライブラリでは適応刻み幅制御が実装されているので、 $\Delta t$ を直接指定しません。代わりに、解の精度を指定します。この精度を高めにとらないと、不安定性の影響が出ます。上の例では、相対誤差 rtol=1e-8 を指定しましたが、デフォルト値のまま（rtol=1e-3）計算すると、下図のように明らかにおかしな結果となります（適応刻み幅制御により、おかしくなった後も発散はせずに持ちこたえています）。

このようなおかしな結果が得られたら、公式ドキュメントを参照して、精度や $\Delta t$ に関連したパラメータがないか探してください。公式ドキュメントを参照する習慣をつけておくことがとても重要です。