3.5. 【例題】強相関電子系（ハバード模型）¶

3.5.1. ハバード模型 ¶

金属や半導体中の電子の性質を考える際には、電子間のクーロン斥力を無視した（あるいは平均場として考慮した）理論がよい出発点となります。しかし、遷移金属元素や希土類元素を含む強相関電子系と呼ばれる化合物では、電子間のクーロン斥力が重要になってきます。そこで、遮蔽された短距離クーロン斥力を考慮したハバード模型が研究でよく用いられます。

(1)¶ $\mathcal{H} = -\sum_{ij\sigma} t_{ij} c_{i\sigma}^{\dag} c_{j\sigma} -\mu \sum_{i\sigma} n_{i\sigma} + U \sum_i n_{i\uparrow} n_{i\downarrow}$

ここで、 $i, j$ は格子点を区別するラベル（原子の位置を格子上の点で表してサイトと呼ぶ）、 $\sigma$ はスピン成分（ $\uparrow$ または $\downarrow$ ）、 $c_{i\sigma}^{\dag}$ と $c_{i\sigma}^{\dag}$ はそれぞれ電子の生成演算子と消滅演算子、 $n_{{i\sigma}}=c_{i\sigma}^{\dag}c_{i\sigma}$ は粒子数演算子です。

多体模型なので、簡単に対角化できないのは【例題】スピン演算子と同様ですが、ハバード模型では電荷（電子の運動）の自由度がある分、さらに難しくなっています。サイト数N=1, 2の場合に、pythonでどのように対角化できるか見てみます。

3.5.2. 1サイト模型 ¶

まずは簡単のため、N=1から考えます。この場合、ハミルトニアン (1) は

(2)¶ $\mathcal{H} = -\mu (n_{1\uparrow} + n_{1\downarrow}) + U n_{1\uparrow} n_{1\downarrow}$

となります。運動エネルギーが消えて、粒子数演算子だけで書かれているので、固有エネルギーは簡単に求まります。状態は全部で $| 0 \rangle$ , $| \uparrow \rangle$ , $| \downarrow \rangle$ , $| \uparrow\downarrow \rangle$ の4つあり、エネルギーはそれぞれ0, $-\mu$ , $-\mu$ , $-2\mu+U$ です。

実装 ¶

ソースコード hubbard_1site.py

生成・消滅演算子の行列表示を作ります。 4次元の状態空間をスピンごとに分けて、アップスピンがいる・いない×ダウンスピンがいる・いない、の2次元×2次元と考えます。式で書くと、 $\big( |0\rangle \oplus |\uparrow\rangle \big) \otimes \big( |0\rangle \oplus |\downarrow\rangle \big)$ と表せます。各スピンごとの2次元空間で演算子を2×2行列として作り、それをクロネッカー積で組み合わせて4次元に拡張する方針で実装します。【例題】スピン演算子の場合と同じ方針です。

def make_local_ops():
    ops = {}

    # c^+
    cdag = np.zeros((2,2))
    cdag[1, 0] = 1
    ops['c^+'] = cdag

    # c
    c = cdag.transpose()
    ops['c'] = c

    # I
    ops['I'] = np.identity(2)

    # F (for fermionic anticommutation)
    ops['F'] = np.diag((1.0, -1.0))

    return ops

配列生成に使っているNumPyの関数は、【例題】スピン演算子の場合と同じなので、説明は省略します。最後のFと名前の付いた演算子は、あとでフェルミオンの交換関係を表すために使います。

クロネッカー積を使って2つの2×2行列から4×4行列を作る関数は、【例題】スピン演算子の make_matrix 関数を使いまわせますが、ここでは少し拡張しておきます。次のように定義して、任意の数の行列を受け取れるようにします：

def make_matrix(*ops):
    r = 1.0
    for op in ops[::-1]:
        r = np.kron(op, r)
    return r

*ops は 可変長引数 （variable positional arguments）と呼ばれる記法で、任意の個数の引数を受け取って、タプルとして格納します。 29行目：ops[::-1] はタプル（またはリスト）を逆順に取り出す記法です。これにより、後ろの行列から順に numpy.kron で掛け合わされていきます。例えば、ops=(op1, op2, op3) の場合、上記のコードは r = kron(op1, kron(op2, kron(op3, 1.0))) と等価です。

注釈

可変長引数にはvariable positional argumentsとvariable keyword argumentsの2種類あります。両方同時に使用することもでき、関数を func(*ags, **kwargs) のように定義します（前者がpositional、後者がkeyword）。例えば、func(1, 2.5, a=3.0, b=4) と呼び出すと、最初の2つの引数はタプルとして args=(1, 2.5) に格納され、後ろの2つは辞書として kwargs={'a': 3.0, 'b': 4} に格納されます。

さて、ここまで準備ができたら、演算子の4次元ベクトル空間における表現、そしてハミルトニアン行列を作ります。

def solve_hubbard_1site(U, mu=0):

    local_ops = make_local_ops()
    cdag = local_ops['c^+']
    I = local_ops['I']
    F = local_ops['F']

    # creation operators
    Cdag = {}
    Cdag['1u'] = make_matrix(I, cdag)  # F represents fermionic anticommutation
    Cdag['1d'] = make_matrix(cdag, F)

    C = {}  # annihilation operators
    N = {}  # number operators
    for key, cdag in Cdag.items():
        C[key] = hermite_conjugate(cdag)
        N[key] = cdag @ C[key]

    hamil = U * N['1u'] @ N['1d'] - mu * (N['1u'] + N['1d'])
    print("H =\n", hamil)

    eigval, eigvec = np.linalg.eigh(hamil)

    return eigval, eigvec

47～48行目：生成演算子を作っています。フェルミオンの反交換関係を考慮に入れるために、cdag よりも左側には単位行列 I ではなく、F をおきます。 F と I は逆でも問題ありません。

注釈

演算子 F について　ー　【例題】スピン演算子の場合は、異なるラベル（1, 2など）を持つスピン演算子が交換したので、空いている部分には単位演算子 I があるものと解釈しました。フェルミオンの場合は、異なるラベル（サイト、スピン）を持つ演算子が 反交換 するので、異なるラベルを持つ電子が存在する場合に符号が反転するように、F 演算子をおきます。

具体的に、4つの状態ベクトル $|0\rangle$ , $| \uparrow \rangle = c_{\uparrow}^{\dag} |0 \rangle$ , $| \downarrow \rangle = c_{\downarrow}^{\dag} |0 \rangle$ , $| \uparrow \downarrow \rangle = c_{\uparrow}^{\dag} c_{\downarrow}^{\dag} |0 \rangle$ に対して、生成演算子の行列要素を書き下すと

$c_{\uparrow}^{\dag} &= \begin{pmatrix} 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \otimes \begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix}\\ c_{\downarrow}^{\dag} &= \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix} \otimes \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$

となります。F 演算子によって、この中のマイナスを表現しています。なお、 $| \uparrow \downarrow \rangle:$ の定義で $c_{\uparrow}^{\dag}$ と $c_{\downarrow}^{\dag}$ を入れ替えると、マイナスの付く部分が変わって、I と F が入れ替わります。

50～51行目：C は消滅演算子、N は粒子数演算子を持つ辞書です。消滅演算子は生成演算子のエルミート共役を取って作ります。

def hermite_conjugate(mat):
    return mat.conj().T

注釈

エルミート共役を取る関数はなぜかNumPyに含まれていないので、複素共役と転置を組み合わせて自分で作ります（35行目）。これについては、例えば Stack Overflow - Conjugate transpose operator ".H" in numpy が参考になります。

あとは、上で示した solve_hubbard_1site 関数にパラメータを与えて呼び出して結果を表示すれば完成です。

def main():
    U = 10.0
    mu = 2

    E, vec = solve_hubbard_1site(U, mu)

    print("\nE =\n", E)

    print("\nEigenvectors =")
    for i in range(vec.shape[1]):
        print(vec[:, i])

結果 ¶

H =
 [[ 0.  0.  0.  0.]
 [ 0. -2.  0.  0.]
 [ 0.  0. -2.  0.]
 [ 0.  0.  0.  6.]]

E =
 [-2. -2.  0.  6.]

Eigenvectors =
[0. 1. 0. 0.]
[0. 0. 1. 0.]
[1. 0. 0. 0.]
[0. 0. 0. 1.]

解析解と一致していることが確認できます。

3.5.3. 2サイト模型 ¶

さて、ここまでは練習です。次に2サイト模型を考えます。 $t_{12}=t_{21}=t$ とすると

(3)¶ $\mathcal{H} = -t\sum_{\sigma} (c_{1\sigma}^{\dag} c_{2\sigma} + c_{2\sigma}^{\dag} c_{1\sigma}) -\mu \sum_{i\sigma} n_{i\sigma} + U ( n_{1\uparrow} n_{1\downarrow} + n_{2\uparrow} n_{2\downarrow})$

実装 ¶

ソースコード hubbard_2site.py

N=1のコードで基本的な関数は作ったので、それを使いまわせば、だいぶ手間が減ります。それらの関数を使用するために、次のように3つの関数をインポートします。

from hubbard_1site import make_local_ops, make_matrix, hermite_conjugate

2サイト模型の固有値、固有関数を返す関数は以下のように書けます：

def solve_hubbard_2site(t, U, mu=0, n=None):

    local_ops = make_local_ops()
    cdag = local_ops['c^+']
    I = local_ops['I']
    F = local_ops['F']

    # creation operators
    Cdag = {}
    Cdag['1u'] = make_matrix(I, I, I, cdag)
    Cdag['1d'] = make_matrix(I, I, cdag, F)
    Cdag['2u'] = make_matrix(I, cdag, F, F)
    Cdag['2d'] = make_matrix(cdag, F, F, F)

    C = {}  # annihilation operators
    N = {}  # number operators
    for key, cdag in Cdag.items():
        C[key] = hermite_conjugate(cdag)
        N[key] = cdag @ C[key]

    hamil = 0
    # t
    for key1, key2 in [('1u', '2u'), ('1d', '2d'), ('2u', '1u'), ('2d', '1d')]:
        hamil += -t * Cdag[key1] @ C[key2]
    # U
    for key1, key2 in [('1u', '1d'), ('2u', '2d')]:
        hamil += U * N[key1] @ N[key2]
    # mu
    for n_op in N.values():
        hamil += -mu * n_op
    # print("H =\n", hamil)

    if n is not None:
        # projection to n-particle state
        hamil = projection(hamil, n)

    eigval, eigvec = np.linalg.eigh(hamil)

    return eigval, eigvec

24～27行目：生成演算子を作ります。make_matrix 関数が4つの2×2行列を受け取って、16×16行列を返します。4つの引数は、2d, 2u, 1d, 1u の順番に対応していて、生成演算子に対応する成分に cdag を、それより左には単位行列 I を、右にはフェルミオンの反交換を表す行列 F を入れます。

29～33行目：消滅演算子と粒子数演算子を作る部分は、N=1の場合と同じです。

35～44行目：各種演算子を表す16×16行列の積や和を組み合わせてハミルトニアンを作ります。

47～49行目：関数の第4引数に整数 n が与えられた場合に、ハミルトニアンを特定の粒子数 n の空間へ射影します。詳細は後で説明します。

結果 ¶

$t=1, U=4, \mu=2$ とした場合のエネルギー固有値の結果です。

E =
 [-4.82842712e+00 -4.00000000e+00 -4.00000000e+00 -4.00000000e+00
 -3.00000000e+00 -3.00000000e+00 -3.00000000e+00 -3.00000000e+00
 -1.00000000e+00 -1.00000000e+00 -1.00000000e+00 -1.00000000e+00
 -4.89361506e-17  0.00000000e+00  0.00000000e+00  8.28427125e-01]

全部で16個のエネルギー固有値が表示されます。基底状態が1重項、第一励起状態が3重項になってます。

粒子数射影 ¶

この結果だけだと、各エネルギー状態がどんな状態なのか分かりずらいですね。そこで16個の状態を異なる粒子数ごとに分けましょう。全粒子数nは保存量（全粒子数演算子がハミルトニアンと可換）なので、粒子数で固有状態を分けることができます。

def projection(h, n):
    from itertools import product
    # occup = [sum(state) for state in product([0, 1], repeat=4)]
    # index = [i for i, occ in enumerate(occup) if occ == n]
    index = [i for i, state in enumerate(product([0, 1], repeat=4)) if sum(state)==n]
    return h[index, :][:, index]

全粒子数状態を含むハミルトニアン h を与えて、粒子数 n の状態のブロックのみを取り出す関数です。 11行目：リスト内包表記 という記法を使って、全16個の状態から、状態数が n の要素のリストを作成しています。少し詳しく説明します。 itertools.product は多重ループを生成する関数です。この場合、[0, 1] を4回重ねたループが生成されます。つまり、i, state には

0, (0, 0, 0, 0)
1, (0, 0, 0, 1)
2, (0, 0, 1, 0)
...
15, (1, 1, 1, 1)

の16種類の値が順番に入ります。 if sum(state)==n は粒子数が n に一致した場合にのみforループの中身（for の前の命令）を実行するという意味で、これにより、粒子数nに対応するインデックス i のリストが生成されます。例えば、n=0の場合は index=[0,]、n=1の場合は index=[1,2] となります。 12行目：スライス記法を使って、行列から必要な成分のみを取り出した行列を作ります。

n=2とした場合の結果は次の通りです：

E =
 [-4.82842712e+00 -4.00000000e+00 -4.00000000e+00 -4.00000000e+00
  3.84373367e-16  8.28427125e-01]

先の結果の基底状態と第一励起状態はn=2の状態であったことがわかりました。

U依存性 ¶

最後に、クーロン斥力Uを変化させたグラフを描いてみます。

ソースコード hubbard_2site_Udep.py

物理的に重要なn=2の6状態のみを取り出した結果はこちらです（ $\mu=0$ としています）。

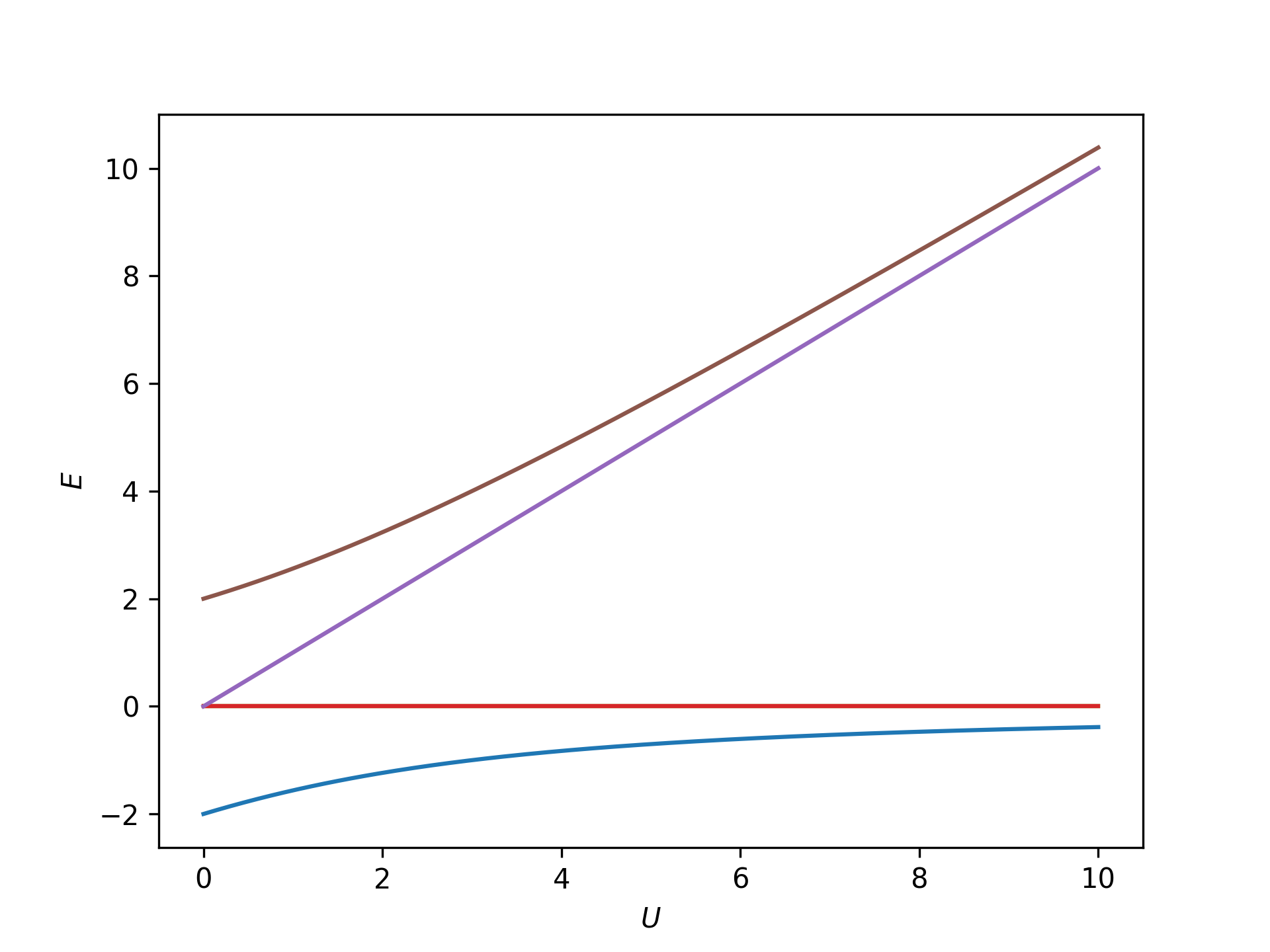
$U\neq0$ における縮退度は、エネルギーの低い方から1重、3重、1重、1重です。

高エネルギーの2状態は、電子が片方の格子点に偏った状態です。クーロン斥力 $U$ の分だけエネルギーが高くなっています。

低エネルギーの4状態は、クーロン斥力を避けて、電子がサイト1と2にひとつずつ存在している状態です。基底状態はスピン一重項状態、励起状態はスピン三重項状態です。一重項と三重項のエネルギー分裂は、 $t$ に関する2次摂動で理解できて、 $4t^2/U$ となることが知られています。 $U$ の大きい領域では、【例題】スピン演算子の2スピン模型が2サイトハバード模型の有効模型になっているということです。

3.5. 【例題】強相関電子系（ハバード模型）¶

3.5.1. ハバード模型 ¶

3.5.2. 1サイト模型 ¶

実装 ¶

結果 ¶

3.5.3. 2サイト模型 ¶

実装 ¶

結果 ¶

粒子数射影 ¶

U依存性 ¶

目次

前のトピックへ

次のトピックへ