3.2. 【例題】量子非調和振動子の固有状態¶

3.2.1. シュレディンガー方程式 ¶

時間に依存しないシュレディンガー方程式を考えます。

(1)¶ $\left[ -\frac{\hbar^2}{2m} \frac{d^2}{dx^2} + V(x) \right] \psi(x) = E \psi(x)$

この固有値方程式はポテンシャル $V(x)$ が簡単な形の場合には解析的に解けますが、一般的には解くことができません。そこで、数値計算を使って解いてみましょう。

ここではポテンシャルとして以下の関数形を考えます：

(2)¶ $V(x) = \frac{1}{2} m \omega^2 x^2 + \alpha x^4$

第1項は調和振動子のポテンシャル、第2項は非調和項です。 $\alpha=0$ であれば調和振動なので簡単に解くことができますが、 $\alpha \neq0$ の場合は非調和振動となり解析的には解けません。固有エネルギーや固有関数が $\alpha$ によってどのように変化するかを調べてみましょう。

3.2.2. 無次元化 ¶

「さっそくプログラミングしよう」と始める前にいったん落ち着いて、無次元化 の作業を必ず行います。数値計算をする際には無次元化の習慣をつけてください。

物理系の方程式は各変数や係数が次元を持っています（時間とか長さとかのこと。 $x$ なら長さ、 $t$ なら時間など）。コンピュータで扱う変数はただの数なので、「1」が何を表すのかを明確にしなければなりません。そのために、規準となる量を決めて、その量で変数や係数を割っておきます。これを無次元化と呼びます。実際の物理系と対応付けたいときには、その物理系の規準量の大きさで全ての結果をスケールしてやります。

今考えている方程式 (1) + (2) の場合は、調和振動子極限（ $\alpha=0$ ）のエネルギー量子 $\hbar \omega$ を基準にするのが分かりやすいでしょう。対応する長さは $a=\sqrt{\hbar/m\omega}$ です。これらの量でエネルギーと空間座標をそれぞれ無次元化した新しい変数を導入します。

$\epsilon = \frac{E}{\hbar \omega}, \quad \xi = \frac{x}{a}$

これらの無次元変数を使うと、固有値方程式は

$\left[ \frac{1}{2} \left( -\frac{\xi^2}{d\xi^2} + \xi^2 \right) + \alpha' \xi^4 \right] \psi = \epsilon \psi$

と書き換えられます。 $\alpha'$ は $\alpha'=\hbar \alpha / m^2 \omega^3$ で定義される非調和性を特徴づける無次元パラメーターです。元々の方程式は3つのパラメーター（ $m, \omega, \alpha$ ）を持っていましたが、無次元化することで、実は1つのパラメーターだけで解が決まることがわかります。

3.2.3. 実装 ¶

ソースコード anharmonic.py

まずはポテンシャル行列を作ります。そのために、実空間メッシュ $\xi_0, \xi_1, \cdots, \xi_{2n_x-1}$ を持つ1次元配列（ベクトル）とそのベクトルの各成分の2乗、4乗を持つベクトルを作ります。

    # arrays containing x, x^2, x^4
    x = np.linspace(-x_max, x_max, 2*nx)
    x2 = x**2  # element-wise square
    x4 = x2**2

numpy.linspace を使って、領域[ -x_max, x_max ]を等分割した配列を生成しています（点の数が 2*nx なので、2*nx-1 等分になります）。 34行目：NumPyでは配列同士の掛け算は成分ごとの掛け算と定義されているので、x*x で各成分を2乗した配列が得られます（x**2 でも同じ結果になります）。

注釈

NumPy配列同士の四則演算と比較演算は 成分ごと（element-wise） です。リファレンスマニュアルのこちらに記述があります。

Arithmetic and comparison operations on ndarrays are defined as element-wise operations, and generally yield ndarray objects as results.

具体的に、arithmetic operationsは +, -, *, /, //, %, divmod(), **, pow(), <<, >>, &, ^, |, ~ を、 comparison operationsは ==, <, >, <=, >=, != を意味します。

x2, x4 からポテンシャル $V(x_i)$ をベクトルとして作り、それを対角成分として持つ行列を生成します。

    # potential term
    v_diag = 0.5 * x2 + anharmonicity * x4
    v_matrix = np.diag(v_diag)

配列 numpy.ndarray に数値を掛ける操作は各成分への掛け算として定義されています。また、配列同士の足し算は成分ごとの足し算となります。このように直感的に書けるのがpythonのいいところです。最後の行で、numpy.diag を使ってベクトルから対角行列を生成しています。

注釈

numpy.diag はベクトルを与えると対角行列を生成し、行列を与えると対角成分をベクトルとして抽出する、という2つの異なる動作をする関数なので気を付けましょう。また、似た名前の numpy.diagonal という関数もありますが、そちらは対角成分の抽出のみの動作となっています。少々ややこしいですが、その都度公式ドキュメントを見て動作を確認しましょう。

次に、運動エネルギー部分を作ります。 2階微分の中心差分は、2次精度では

$f''(x_i) &= \frac{1}{h^2} (f_{i+1} - 2f_{i} + f_{i-1}) + \mathcal{O}(h^2)$

で与えられるので、 $\frac{d^2}{d\xi^2}$ の行列表示 $D_{xx}$ は

$D_{xx} = \frac{1}{h^2} \begin{pmatrix} -2 & 1 & 0 & 0 & \cdots & 0 & 1 \\ 1 & -2 & 1 & 0 & & & 0\\ 0 & 1 & -2 & 1 & \ddots & & \vdots \\ \vdots & 0 & 1 & -2 & \ddots & \ddots & \vdots \\ \vdots & & \ddots & \ddots & \ddots & \ddots & 0 \\ 0 & & & \ddots & \ddots & -2 & 1 \\ 1 & 0 & \cdots & \cdots & 0 & 1 & -2 \end{pmatrix}$

となります（差分を参考）。これを使うと、運動エネルギーは以下のように実装できます：

def make_second_deriv(dim, dx):

    # make a diagonal matrix its shifted ones (periodic boundary condition is assumed)
    f0 = np.identity(dim, dtype=int)  # f_{i}
    f1 = np.roll(f0, 1, axis=1)  # f_{i+1}
    f2 = np.roll(f0, 2, axis=1)  # f_{i+2}
    f_1 = f1.transpose()  # f_{i-1}
    f_2 = f2.transpose()  # f_{i-2}

    # O(dx^2): (f_{i+1} - 2f_{i} + f_{i-1}) / dx^2
    deriv2 = (f1 - 2.0 * f0 + f_1) / (dx*dx)

    # O(dx^4): [(-1/12)f_{i+2) + (4/3)f_{i+1} - (5/2)f_{i} + (4/3)f_{i-1} - (1/12)f_{i-2}] / dx^2
    # deriv2 = ((-1./12.)*f2 + (4./3.)*f1 - (5./2.)*f0 + (4./3.)*f_1 - (1./12.)*f_2) / (dx*dx)

    return deriv2

コードを見やすくするために、行列を作る関数を別に定義しています（ここでは続けて書いています）。まず、numpy.identity で単位行列を用意して（13行目） numpy.roll でそれを右・左にシフトした行列を作り（14～15行目）、それらの和で目的の行列 $D_{xx}$ を作っています（20行目）。このような規則的な行列なら、行列要素に直接アクセスせずに、NumPyの関数だけで作れます。

あとは、ポテンシャル行列と微分演算子を足し合わせればハミルトニアン行列の完成です。

    # Hamiltonian
    h_matrix = v_matrix + kin_matrix

    # diagonalize
    print("diagonalizing Hamiltonian...")
    eigval, eigvec = linalg.eigh(h_matrix)

    # normalize eigenvectors so that the result does not depend on dx
    eigvec /= np.sqrt(dx)

対角化にはエルミート行列の対角化関数 numpy.linalg.eigh を使っています。固有値が実数、固有ベクトルがユニタリーであることが保証されます。また、固有値が小さい順に整列される点も便利です。最後の行では、固有ベクトルが dx に依存しないようにスケールしています。

最後に、固有関数をファイルに保存しておきます。

    # save result for eigenvalues
    print("saving results...")
    np.savetxt(file_val, eigval)

    # save result for eigenvectors
    temp = np.hstack([x[:, None], eigvec[:, 0:n_vec]])
    np.savetxt(file_vec, temp)

NumPyの配列をファイルに書き出すには numpy.savetxt を使うのが便利です。第一引数にファイル名、第二引数に配列を与えます。固有値は1次元配列なので、そのまま関数に与えて問題ないです。一方、固有ベクトルの書き出しは、後でグラフを描きやすいように少し工夫しています。numpy.hstack という関数を使って1列目に座標、2列目以降に固有ベクトルが並ぶような2次元配列を作ってから numpy.savetxt に与えています。

注釈

x[:, None] は1次元配列を2次元配列に変換する書き方で、Noneは numpy.newaxis と等価です。

The newaxis object can be used in all slicing operations to create an axis of length one. newaxis is an alias for ‘None’, and ‘None’ can be used in place of this with the same result.

62行目：eigvec[:, 0:n_vec] ではスライス機能を使って低エネルギーの n_vec 個だけ固有ベクトルを抜き出すようにしています。

3.2.4. 結果 ¶

ここでは、調和振動子（ $\alpha=0$ ）の結果を示し、解析解との比較をします。非調和項 $\alpha$ が入った場合に固有値や固有関数がどのように変わるかはサンプルスクリプトを使って確かめみてください。

固有エネルギー ¶

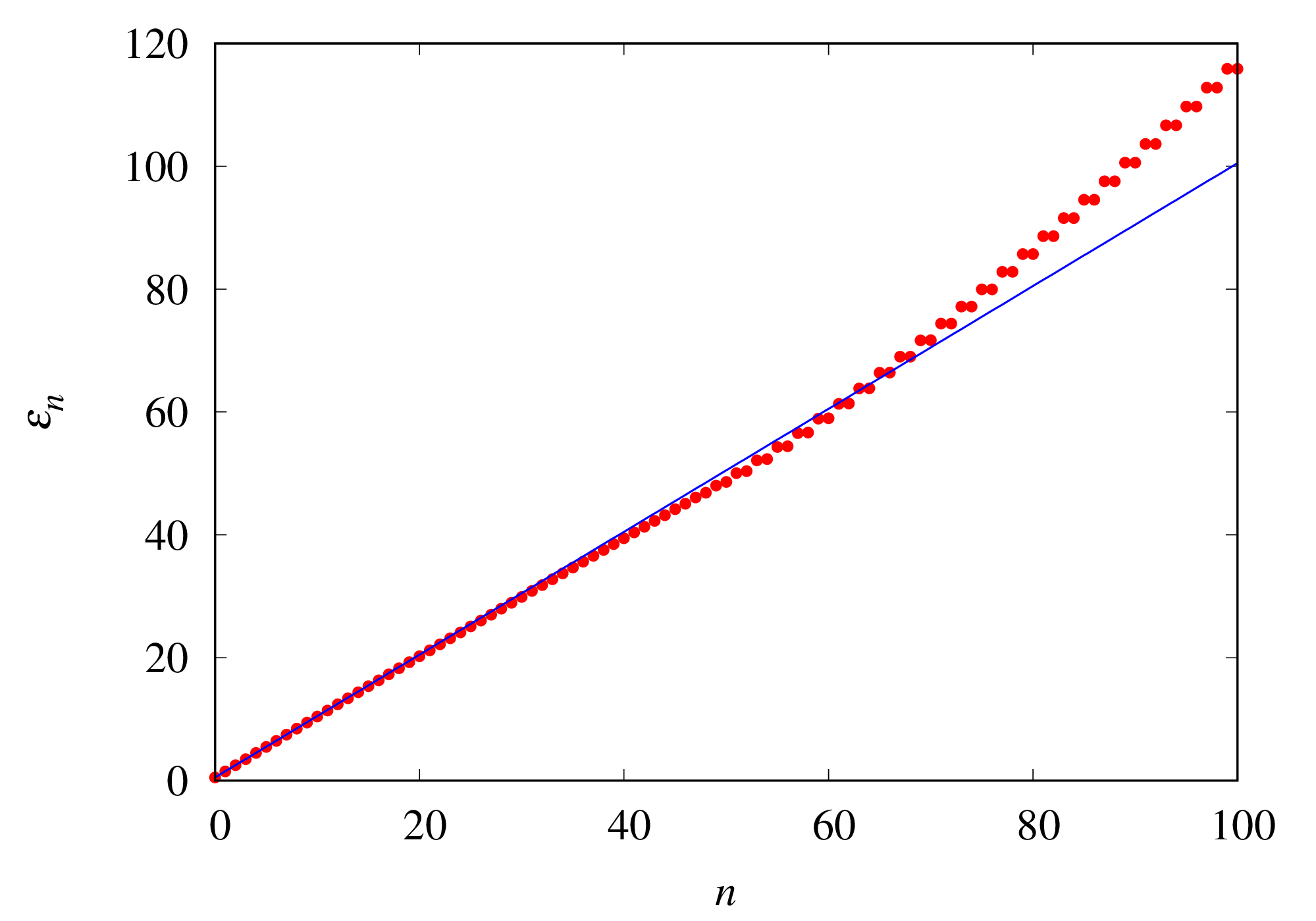
赤点が数値結果、青線が解析解 $\epsilon_n = n + 1/2$ です。 $n\lesssim 20$ で良い一致が見られます。 $n\gtrsim 20$ で解析解からのズレが見られるのは、(1) 波動関数の節が多くなって差分の誤差が無視できなくなったため、(2) 波動関数の広がりが端まで達して端の影響が出てしまったため、の2つが考えられます。

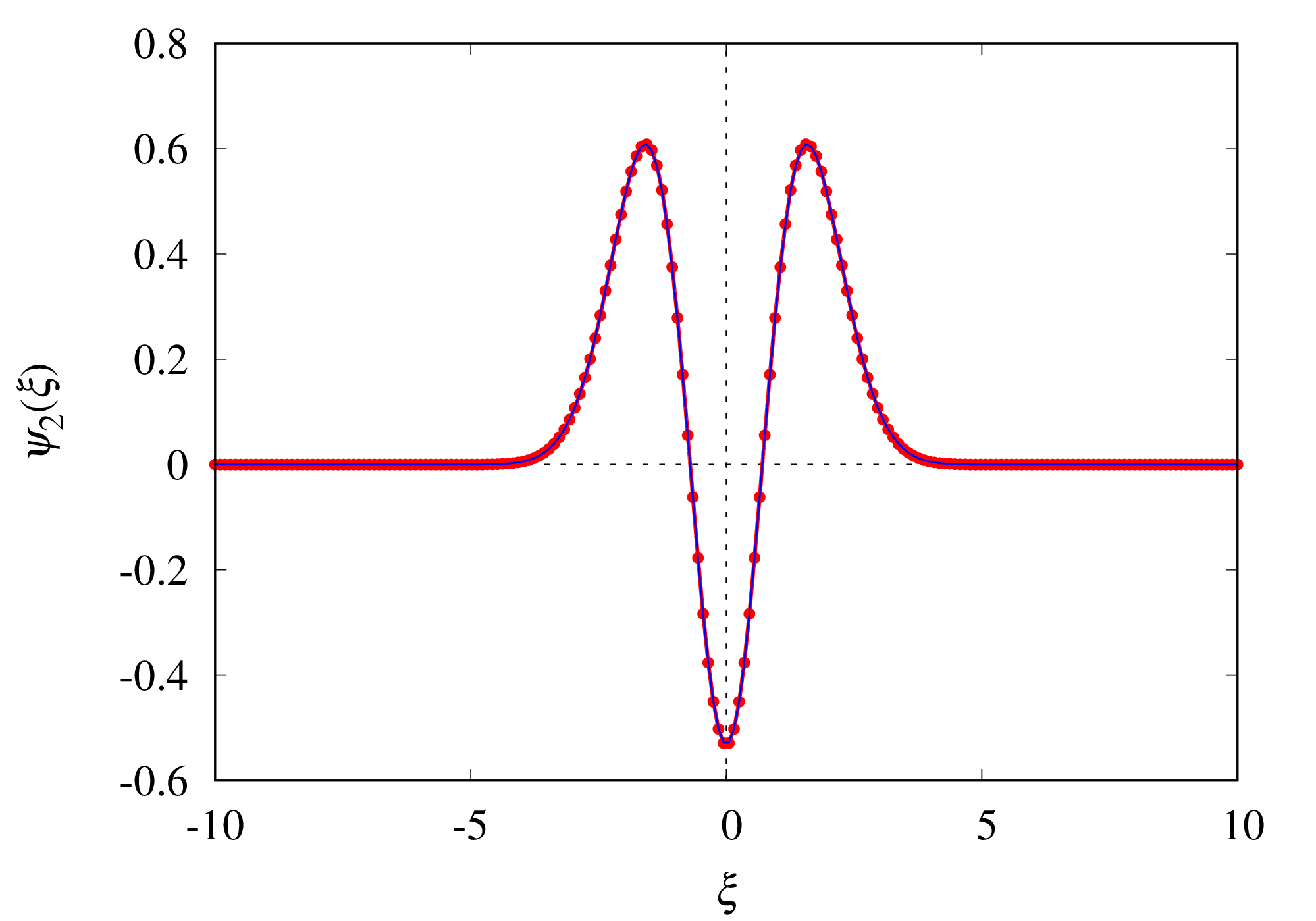
固有関数 ¶

$n=2$ の固有関数を解析解（エルミート多項式）と比較します。完全に一致していることが確認できます。

3.2.5. 【発展】精度保証 ¶

数値計算では、得られた結果がどの程度正しいのかを知ることが重要です。例えば、上の固有エネルギーの図では、解析解を知っているので「 $n\lesssim 20$ は正しい」と結論できましたが、一般には解析解は利用できません（当然ですが）。正しい答えを知らない問題に対して、自分の答えの正しさを知るにはどうすればよいでしょうか。

今回の例では、メッシュの刻み幅 $h$ を減らして、解が変わらないことを確認するのが最も簡単です。例えば、x座標の分割数 nx を100, 200, 400, 800, 1600と2倍づつ増やしてメッシュを細かくしていった時の、基底状態のエネルギー $\epsilon_0$ を並べると

996841517586778081e-01
999214705696021221e-01
999804190636953360e-01
999951110299039048e-01
999987785322591027e-01

となります。このように比較することで、どの桁まで収束しているかが確認できます（図示するとさらに良いです）。

より精密な議論を行うには、誤差の収束を見ます。今回の例では2次の差分公式を使っているので、ある $h$ に対して得られた固有エネルギー $E_n(h)$ と厳密解 $E_n^\mathrm{exact}$ との差は

$E_n(h) - E_n^\mathrm{exact} = \mathcal{O}(h^2)$

と表せます。これを図示できれば一番いいのですが、厳密解が分かりません。そこで、例えば、 $h$ の2倍異なる計算結果の差

$\Delta_n(h) \equiv E_n(h) - E_n(2h)$

を議論します。この量を図示したものが下の図です。

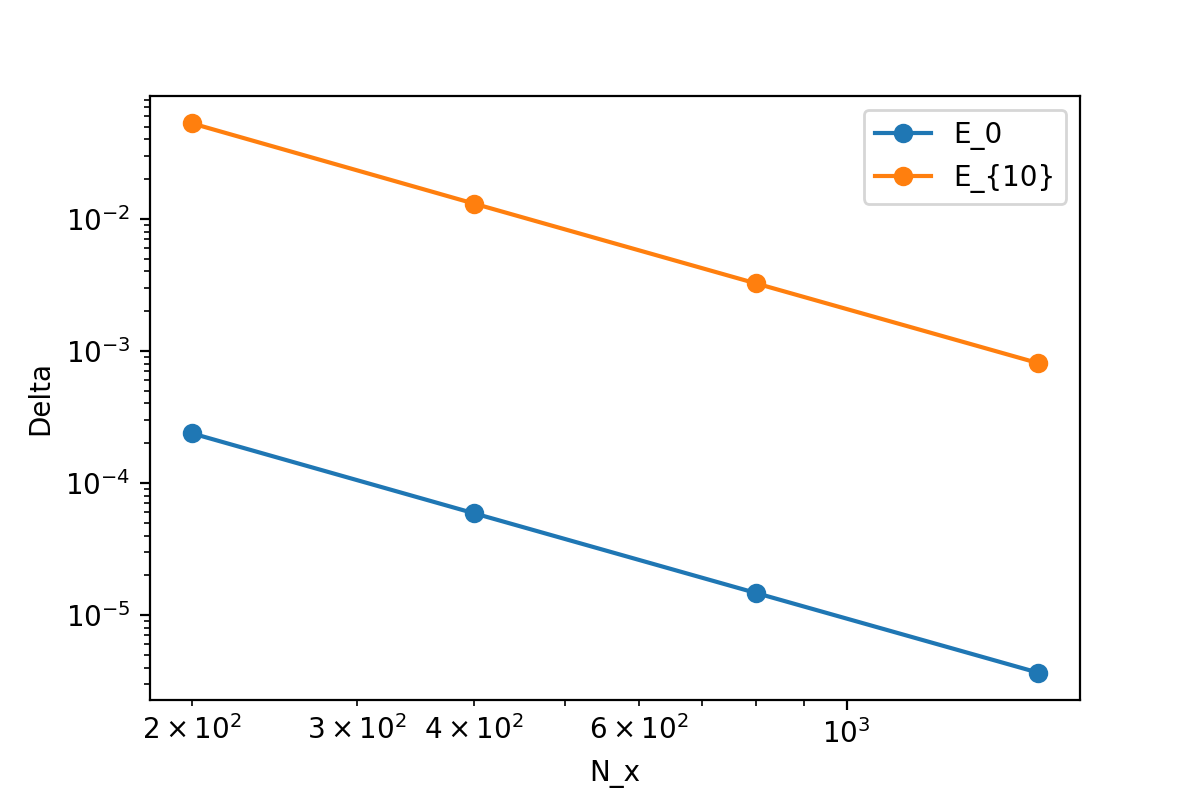
参考のため、n=0に加えてn=10の結果も表示しています。横軸は分割数 $N_x \propto 1/h$ です。誤差のベキ依存性を確認したいので、両対数グラフにしています。 n=0とn=10では傾きが同じですが、切片が違います。これは、誤差のベキが同じ（ $h^2$ ）だけど係数が違うことを意味しています。最大の分割数の場合に、n=0の解の誤差は $10^{-6}$ ほどですが、n=10の解は $10^{-3}$ 程度ということが分かります。また、このグラフを外挿すれば、必要な精度を得るためにはどのくらいの分割数が必要かということも見積もることができます。

3.2. 【例題】量子非調和振動子の固有状態¶

3.2.1. シュレディンガー方程式 ¶

3.2.2. 無次元化 ¶

3.2.3. 実装 ¶

3.2.4. 結果 ¶

固有エネルギー ¶

固有関数 ¶

3.2.5. 【発展】精度保証 ¶

目次

前のトピックへ

次のトピックへ