9.1. 【例題】イジング模型のモンテカルロシミュレーション（作成中）

注釈

モンテカルロシミュレーションは、本当は、pythonで実装するのはあまり適当ではありません。なぜなら、モンテカルロ計算はforループで細かい計算を繰り返すプログラムで、外部ライブラリが計算コストを占めるようなものではないからです。 ここでは、モンテカルロシミュレーションの原理を示すために、あえてpythonで実装しています。ただし、ある程度パフォーマンスを意識して、テクニカルな実装になっている部分があることはご容赦ください。

9.1.1. モンテカルロ法

【例題】イジング模型の平均場近似

9.1.2. 実装

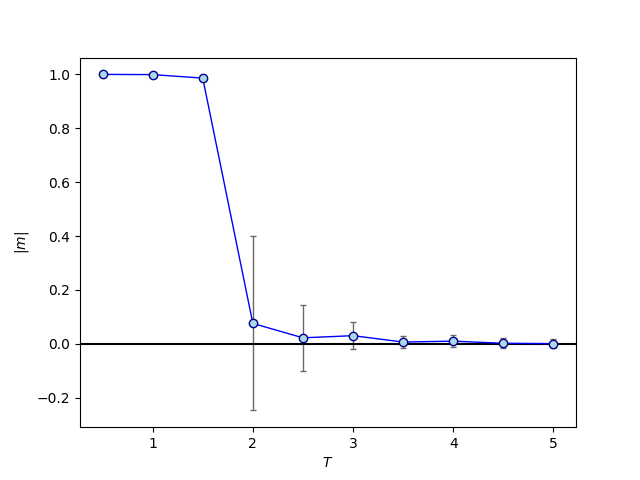
9.1.3. 結果