8.3. 【例題】イジング模型の平均場近似¶
8.3.1. 方程式¶
イジング模型は強磁性相転移を記述する最も簡単な模型です。ハミルトニアンは
で与えられます。
ここで、 は格子点
にあるスピンの状態を表し、+1または-1を取ります(+1が上向き、-1が下向き)。
は隣り合う格子点の組み合わせに関する和を意味します。
この模型は多体模型なので、分配関数を厳密に評価することは、特別な場合を除いてできません。そこで、統計力学の教科書では、平均場近似を適用して一体模型に置き換えて物理量を計算します。
平均場近似では、平均磁化 は以下の自己無撞着方程式を解くことで決定できます:
(1)¶
ここで、 は逆温度、
は最近接格子点の数を表します。
この方程式は
を満たす低温領域で非ゼロの解を持ちます(つまり自発磁化が生じる)。
具体的には、
で
、
で
になることが解析的に示せます。しかし、中間の温度領域では解析的に解けません。数値計算を使ってこの方程式を解き、自発磁化の温度変化を求めます。
磁化 が求まったら、エントロピーと比熱はそれぞれ
から計算できます。ここで、 です。
8.3.2. 実装¶
方程式を解くにはSciPyの scipy.optimize.root_scalar 関数を使います。
scipy.optimize.root_scalarの使い方 で説明したように、まず解きたい関数 f を定義します。
(1) 式を の形に変形して
を返すようにします。
10def func(m, zj, beta, h):
11 return m - np.tanh(beta * (zj * m + h))
第二引数以下はパラメーターです。パラメーターの数値はroot_find関数の args 引数に与えます。
方程式の解を求める関数は以下のように書けます。
14def find_solution(zj, t, h, m_min=1e-6, m_max=1, verbose=False):
15 beta = np.inf if t==0 else 1./t
16 sol = optimize.root_scalar(func, args=(zj, beta, h), method='brentq', bracket=(m_min, m_max))
17 if verbose:
18 print(sol)
19 return sol.root
温度 t から逆温度 beta=1/t の変換では、t=0 の場合に beta=numpy.inf をセットすることで、t=0 も扱えるようにしています。
非線型方程式の解法として、ここでは``method='brentq'`` によりBrent法を指定しています。
Brent法は挟み込むアルゴリズムですので、解の範囲を bracket 引数に与えます。
の解を選ぶような値をデフォルトとしていますが、外部からも変更できるようにしています。
磁場
h がある場合には調整する必要があります。
verbose は詳細な結果を出力するオプションです。計算結果がおかしい場合などに verbose=True として詳細な出力を得るようにします。
あとはこの関数を呼び出せば自己無撞着方程式を満たす解が得られます。
41def main():
42 t = 0.1
43 zj = 1.0
44 h = 0.0
45 m = find_solution(zj, t, h, verbose=True)
46 s = calc_entropy(m)
47 c = calc_specific_heat(m, zj, t)
48 print(f"zJ = {zj}")
49 print(f"T = {t}")
50 print(f"h = {h}")
51 print(f"m = {m}")
52 print(f"S = {s}")
53 print(f"C = {c}")
比熱とエントロピーも計算していますが、特別な計算はしていないので、解説は省きます。ソースコードを見てください。
8.3.3. 出力結果¶
$ python ising_mf.py
converged: True
flag: 'converged'
function_calls: 4
iterations: 3
root: 0.9999999958776924
zJ = 1.0
T = 0.1
h = 0.0
m = 0.999999995878
S = 4.32842296841e-08
C = 8.2446158185e-07
最初の5行は verbose=True としたことによる、詳細の出力です。
m はほぼ1で完全に強磁性状態になっていることが分かります。
パラメーターを変化させて正しい解が得られていることを確認してください。
8.3.4. 温度変化¶
さて方程式を正しく解けていることが確認出来たら、温度変化のグラフを作ってみましょう。
そのために、先ほど作った関数 find_solution は使いまわして、main関数だけを新たに作ります。
t_dep.pyの冒頭で先ほどのファイルをインポートします。
5from ising_mf import find_solution, calc_entropy, calc_specific_heat
これにより、ising_my.pyの中にある find_solution 関数を使えるようになります。ising_mf.pyとt_dep.pyは必ず同じディレクトリにおいてください。そうしないとising_mf.pyを見つけられずにエラーがでます。
あとは温度を変化させながら find_solution を繰り返し呼び出せば完了です。
8def main():
9 h = 0
10 tmin = 0
11 tmax = 1
12 n = 201
13 for t in np.linspace(tmin, tmax, n):
14 try:
15 m = find_solution(1., t, h)
16 s = calc_entropy(m)
17 c = calc_specific_heat(m, 1., t)
18 except ValueError:
19 print(f"# {t:.4f}")
20 else:
21 print(f"{t:.4f} {m:.5e} {s:.5e} {c:.5e}")
解が見つからなかった場合のために、例外処理 をしてあります。 tryブロックでエラー(例外)が発生したら、該当する例外に対応するexceptブロックが実行されます。 もし、該当するexceptブロックが存在しない場合には、プログラムが終了します。 エラーがなくtryブロックが終了した場合には、elseブロックが実行されます。 例外処理 については公式ドキュメントのほか、文献 [2] を参照してください。
8.3.5. 結果&図示¶
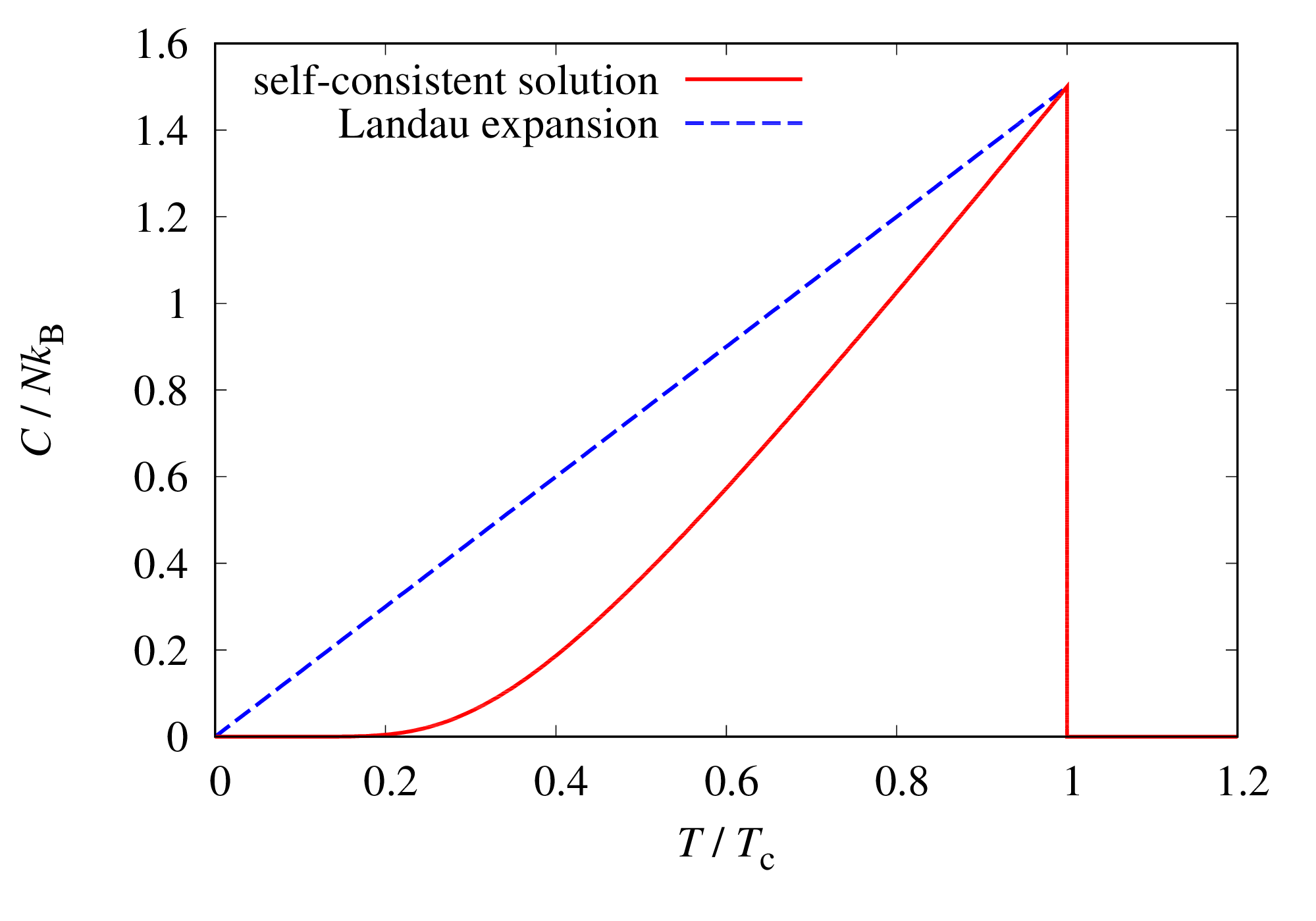
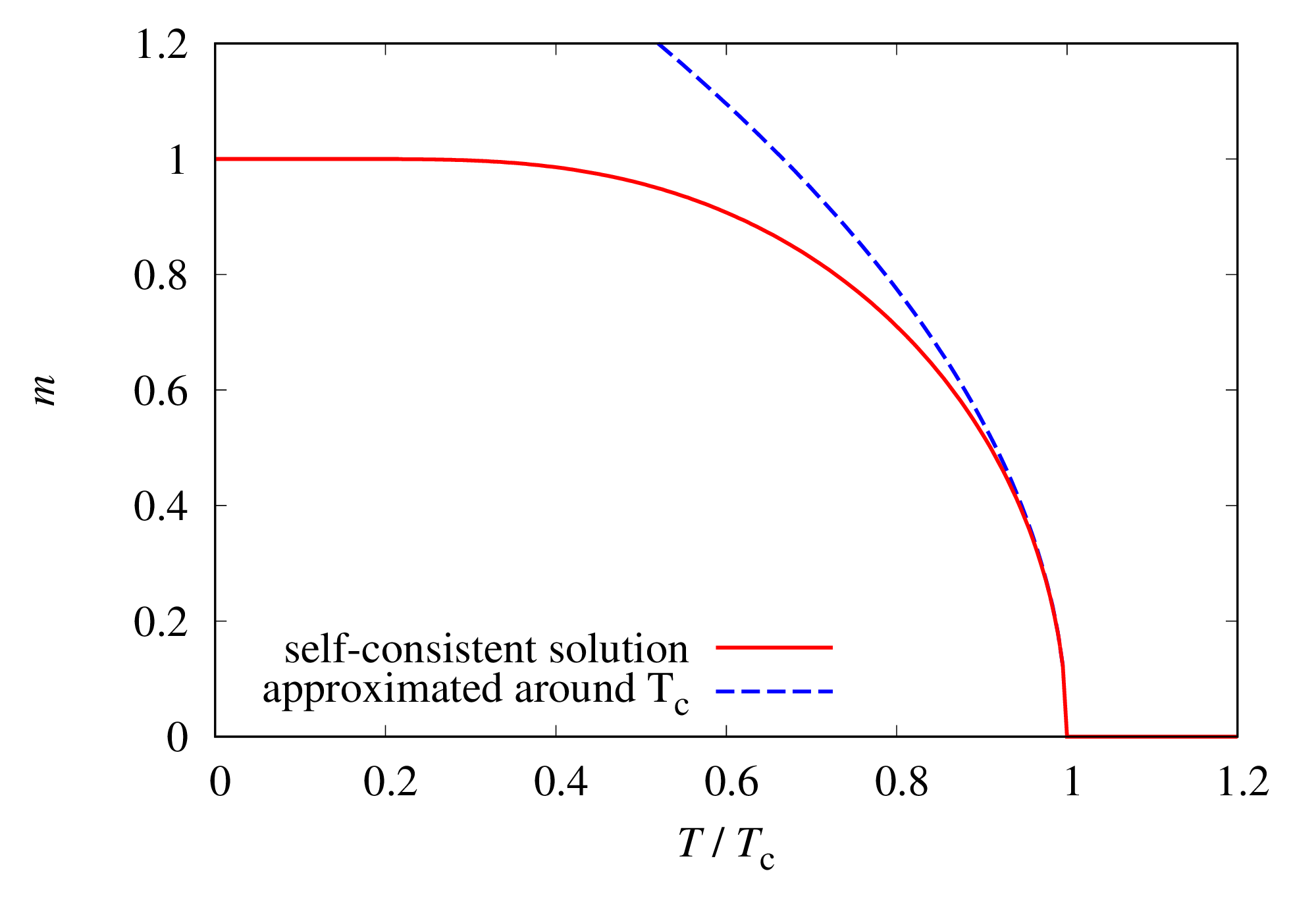
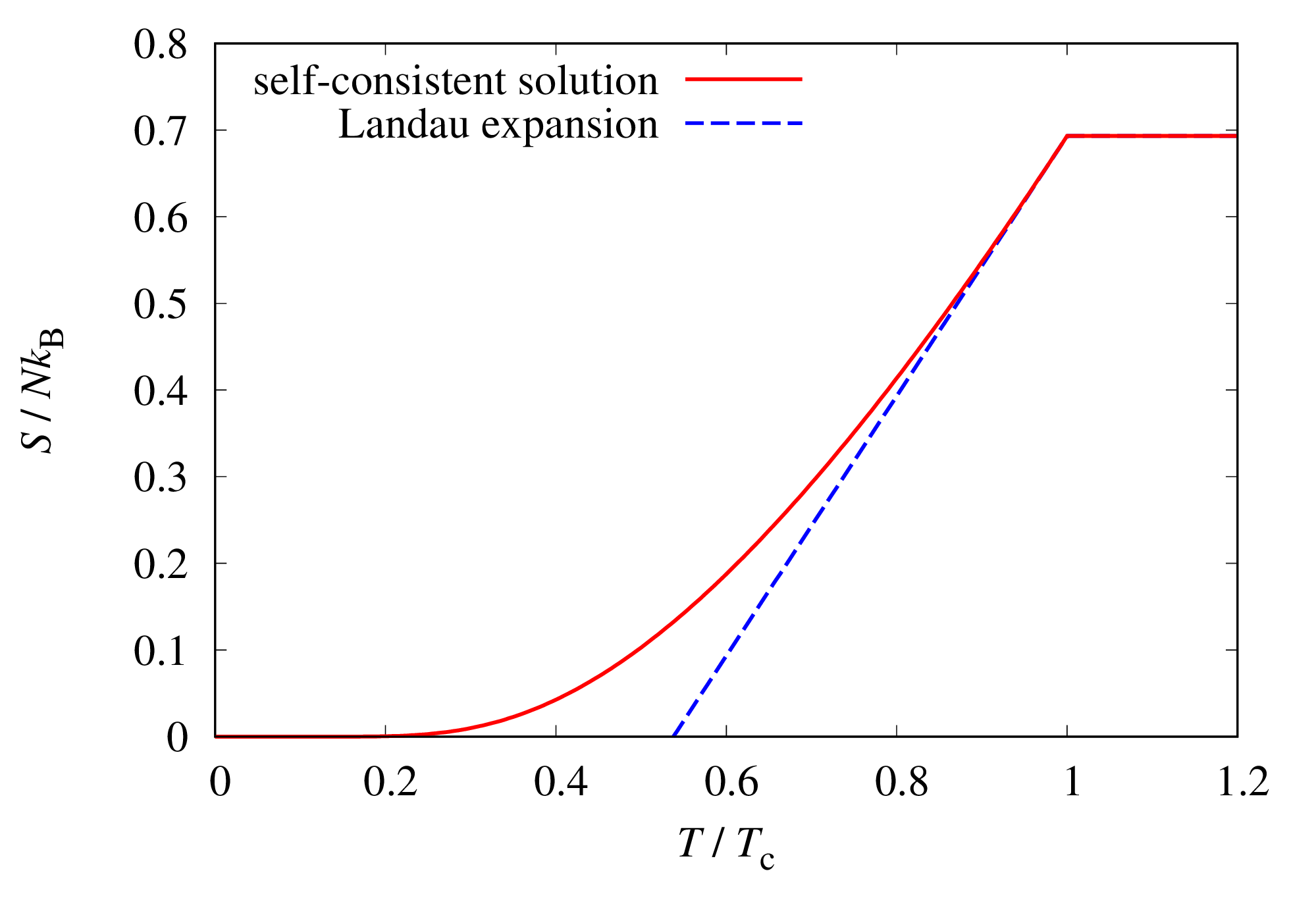
各物理量の温度依存性を図示すると以下のようになります(赤線)。
参考のために、 近傍における解析解を青破線で示しています。
磁化¶
エントロピー¶
比熱¶