8.2. 【例題】ボーズ・アインシュタイン凝縮の比熱

8.2.1. 計算式

理想ボーズ気体におけるボーズ・アインシュタイン凝縮の計算では、ボーズ・アインシュタイン積分と呼ばれる次の積分が登場します：

(1)F_s(\alpha) \equiv \frac{1}{\Gamma(s)} \int_0^{\infty} dx \frac{x^{s-1}}{e^{x+\alpha}-1}

\alpha は化学ポテンシャルを温度によって無次元化した量 \alpha = -\mu/k_\mathrm{B}T です。 ボーズ・アインシュタイン凝縮の転移温度を T_\mathrm{c} とすると、 T<T_\mathrm{c} では \alpha=0 となり、このとき積分は F_s(0)=\zeta(s) のように実行できます。 一方、T>T_\mathrm{c} では 以下の方程式を満たすように \alpha を決定する必要があります：

(2)F_{3/2}(\alpha) = \zeta(\tfrac{3}{2}) t^{-\tfrac{3}{2}}

ここで、t は無次元化した温度 t\equiv T/T_\mathrm{c} です。

\alpha が求まったら各種熱力学量が計算できます。 例えば比熱は

\frac{C}{N k_\mathrm{B}} = \begin{cases} \displaystyle \frac{15}{4} \frac{F_{5/2}(\alpha)}{F_{3/2}(\alpha)} - \frac{9}{4} \frac{F_{3/2}(\alpha)}{F_{1/2}(\alpha)} & (t>1) \\[12pt] \displaystyle \frac{15}{4} \frac{\zeta(\tfrac{5}{2})}{\zeta(\tfrac{3}{2})} t^{3/2} & (t<1) \end{cases}

によって得られます。

積分 (1) と非線型方程式 (2) を数値計算で解き、 比熱の温度依存性を計算します。

8.2.2. 実装

ソースコード bec.py

まず、積分 (1) を計算する関数を用意しておきます。

4from scipy import integrate
5from scipy import special

21def integrand(x, s, alpha):
22    # x+alpha > 0
23    e = np.exp(-x-alpha)
24    return np.power(x, s-1) * e / (1.0 - e)

27def bose_einstein_integral(s, alpha, verbose=False):
28    y, err = integrate.quad(integrand, 0, np.inf, args=(s, alpha))
29    if verbose:
30        print(f"integral : {y}")
31        print(f"error    : {err}")
32    return y / special.gamma(s)

integrand で被積分関数を定義しています。 積分変数 x に加えて、2つのパラメーター s と \alpha を引数に取ります。 被積分関数の分母が x\to\infty で発散してしまうので、 1/(e^{x+\alpha}-1) = e^{-(x+\alpha)}/(1-e^{-(x+\alpha)}) のように式変形をして計算しています。

数値積分にはSciPyの scipy.integrate.quad 関数を使っています。 この関数の使い方については scipy.integrateの使い方 を参照してください。 ガンマ関数はscipyに含まれる関数 scipy.special.gamma を利用しています。

次に、\alpha を決定する方程式 (2) を scipy.optimize.root_scalar を使って解きます。

6from scipy import optimize

35def func_alpha(alpha, t):
36    return bose_einstein_integral(1.5, alpha) * np.power(t, 1.5) - special.zeta(1.5)

39def calc_alpha(t, verbose=False):
40    if t<=1:
41        return 0
42
43    a_min = 0
44    a_max = 100
45    sol = optimize.root_scalar(func_alpha, args=(t,), method='brentq', bracket=(a_min, a_max))
46    if verbose:
47        print(sol)
48    return sol.root

func_alpha で方程式 (2) を定義しています。 このとき、第一引数が決定したい変数 \alpha で第二引数がパラメーターです。 optimize.root_scalar 関数に func_alpha 関数を渡すことで方程式 (2) を満たす \alpha が得られます。

あとは calc_alpha 関数から \alpha を受け取って比熱を計算すれば完成です。

51def calc_specific_heat(alpha, t):
52    if t<=1:
53        z52 = special.zeta(2.5)
54        z32 = special.zeta(1.5)
55        return 15. * z52 / (4. * z32) * np.power(t, 1.5)
56    else:
57        f12 = bose_einstein_integral(0.5, alpha)
58        f32 = bose_einstein_integral(1.5, alpha)
59        f52 = bose_einstein_integral(2.5, alpha)
60        return 15. * f52 / (4. * f32) - 9. * f32 / (4. * f12)

63def solve_bec(t, verbose=False):
64    alpha = calc_alpha(t, verbose=verbose)
65    c = calc_specific_heat(alpha, t)
66    return alpha, c

main関数から solve_bec 関数を呼び出し、結果を表示します。

69def main():
70    t = 1.5
71    alpha, c = solve_bec(t, verbose=True)
72    print(f"alpha = {alpha}")
73    print(f"c = {c}")

8.2.3. 実行結果

$ python bec.py
      converged: True
           flag: 'converged'
 function_calls: 17
     iterations: 16
           root: 0.16114443396626077
alpha = 0.161144433966
c =  1.7103442045884472

8.2.4. 温度変化

ソースコード bec_t.py

温度変化を計算するには、main関数だけ新たに作ります。 ファイルの冒頭にある

from bec import solve_bec

の一文によって、bec.pyファイルの中で定義されている solve_bec 関数がインポートされ使用できるようになります。 ただし、bec_t.pyとbec.pyは同じディレクトリに置く必要があります。

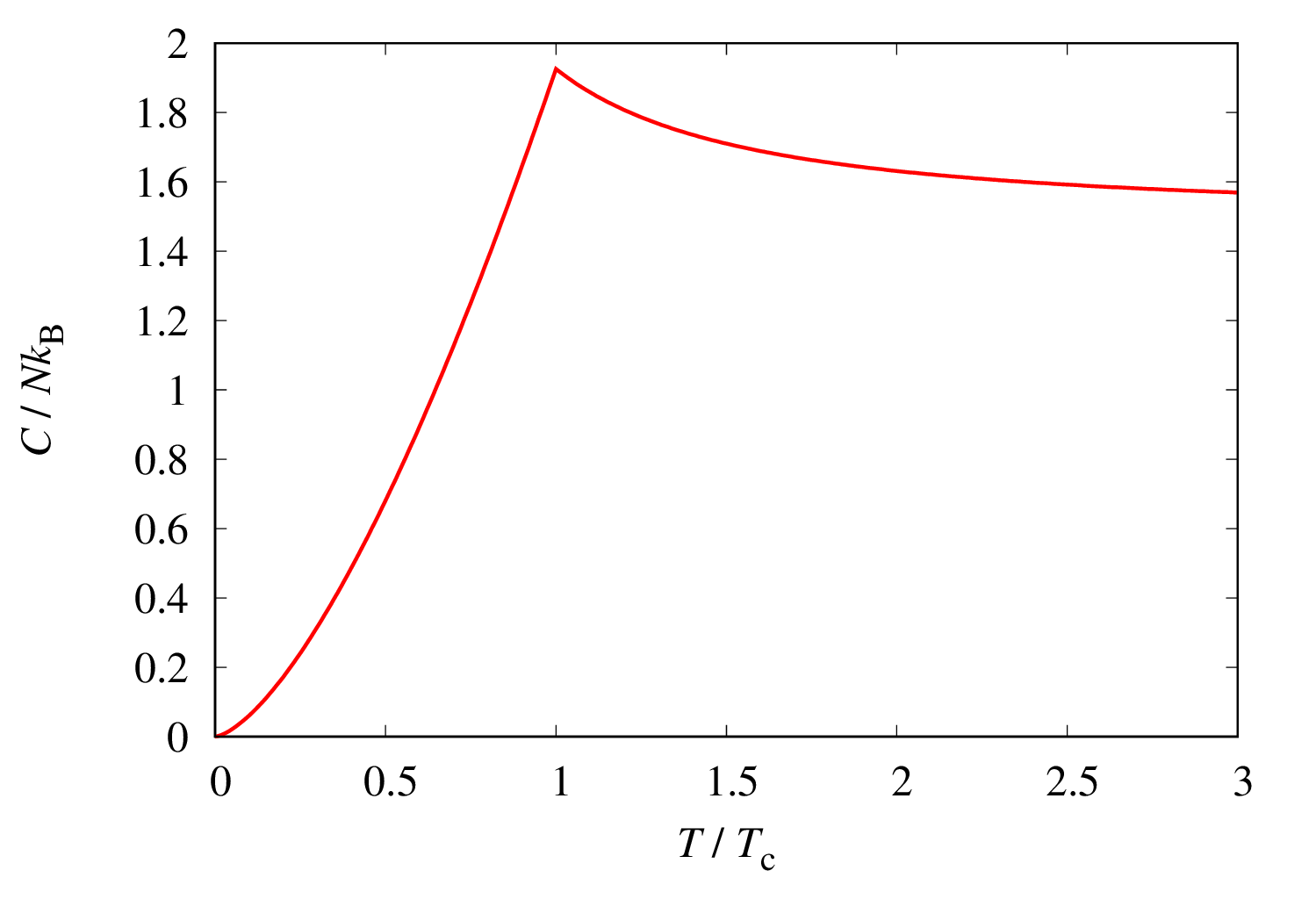
計算結果を図示すると、以下のように、ボーズ・アインシュタイン凝縮の比熱が得られます。

../_images/bec.png