4.2. 【例題】ロジスティック方程式¶

4.2.1. 方程式 ¶

次の方程式はロジスティック方程式と呼ばれます：

(1)¶ $\frac{dy}{dt} = y(1-y)$

これは生物の個体数の増加を表すモデルです。 $y$ は個体数を最大値で規格化した変数で $0<y<1$ を考えます。この方程式を数値的に解いて、関数の使い方や注意点を見ていきます。

方程式の解説 ¶

方程式の意味や解の振る舞い等を簡単に説明しておきます。詳細は Wikipedia を参考にしてください。

まず、生物の繁殖を考えます。個体数の増加率を $\lambda$ とすると、個体数 $Y$ の満たす方程式は

$\frac{dY}{dT} = \lambda Y$

と表されます。解は $Y(T)=Y_0 e^{\lambda T}$ となり、指数関数的な個体数の増加が表されています。

しかし、個体数が少ない時はこれでよいですが、個体数が増えるほど増加率が鈍り、いつかは増加が止まります。これを考慮するために、増加率を $\lambda \to \lambda (1-Y/Y_{\infty})$ で置き換えます。個体数が増えるほど増加率が減ることを表しています。個体数が $Y_{\infty}$ に一致したところで増加が止まります。これを考慮すると、方程式は

$\frac{dY}{dT} = \lambda Y \left( 1- \frac{Y}{Y_{\infty}} \right)$

となります。最後に、 $y\equiv Y/Y_{\infty}$ と規格化、 $t\equiv \lambda T$ と無次元化すると (1) 式が得られます。

方程式 (1) の解は

(2)¶ $y(t) = \frac{y_0}{y_0 + (1-y_0) e^{-t}}$

となります。 $t\to\infty$ で $y \to 1$ に収束します。この関数をロジスティック関数と呼んだりもします。物理ではフェルミ分布関数をひっくり返したものと言った方が通じます。

4.2.2. 実装 ¶

ソースコード logistic_solve_ivp.py

まずは、方程式 (1) の右辺を作ります。

def f_logistic(t, y):
    return y * (1.0 - y)

関数の形は f(t,y) と決まっているので、第1引数の t は使わないですが省略できません（引数を増やすことはできます）。

次に、scipy.integrate.solve_ivp 関数を使って微分方程式解きます。

from scipy.integrate import solve_ivp

このように solve_ivp 関数をインポートしておき、以下のように呼び出します。

def main():
    y0 = np.array([1e-3, ], dtype=float)
    t_start = 0
    t_end = 20.0

    # Solve ODE
    sol = solve_ivp(f_logistic, (t_start, t_end), y0, dense_output=True)
    print(sol.message)
    print("t.shape =", sol.t.shape)  # (n_points,)
    print("y.shape =", sol.y.shape)  # (1, n_points)

これだけです。 16行目：y0 に初期値を入れます。y は1次元配列が想定されているので、y0 は要素数1の1次元配列とします。 21行目：グラフ作成のために、dense_output=True を指定しておきます。

結果は sol オブジェクトが持っています。数値データとして保存します。

    # Save results at selected time points
    filename = "result_original.dat"
    np.savetxt(filename, np.hstack([sol.t[:, None], sol.y.T]))
    print("'{}' generated".format(filename))

sol.t で自動的に選ばれた時刻が得られます（サイズ (n_points,) の1次元配列）。 sol.y でその時刻における結果が得られます（サイズ (n, n_points) の2次元配列；この例では n=1）。 28行目：numpy.savetxt 関数を使ってテキストデータとして保存します。このとき、numpy.hstack を使って sol.t と sol.y を結合してから savetxt に与えます。

sol.t に含まれるデータ点は少なく、グラフ描画には向きません（ソルバーが効率よく時間を進めるため）。グラフ作成用に、時刻を細かく刻んだデータも作成しておきます。任意の時刻における結果は、ソルバーに応じた内挿公式を使って計算されます（ソルバーに dense_output=True を指定しておく）。

    # Save dense output for plot
    nt = 101
    t = np.linspace(t_start, t_end, nt)  # shape (nt,)
    y = sol.sol(t)  # shape (1, nt)
    filename = "result_dense.dat"
    np.savetxt(filename, np.hstack([t[:, None], y.T]))
    print("'{}' generated".format(filename))

numpy.linspace を使って時刻の配列を作り（33行目）、sol.sol(t) で各時刻における結果を得ます（34行目）。

4.2.3. 結果 ¶

The solver successfully reached the end of the integration interval.
t.shape = (14,)
y.shape = (1, 14)
'result_original.dat' generated
'result_dense.dat' generated

1行目が sol.message の出力です。実行結果を文章として説明してくれます。

数値データを図示したものが下の図です。

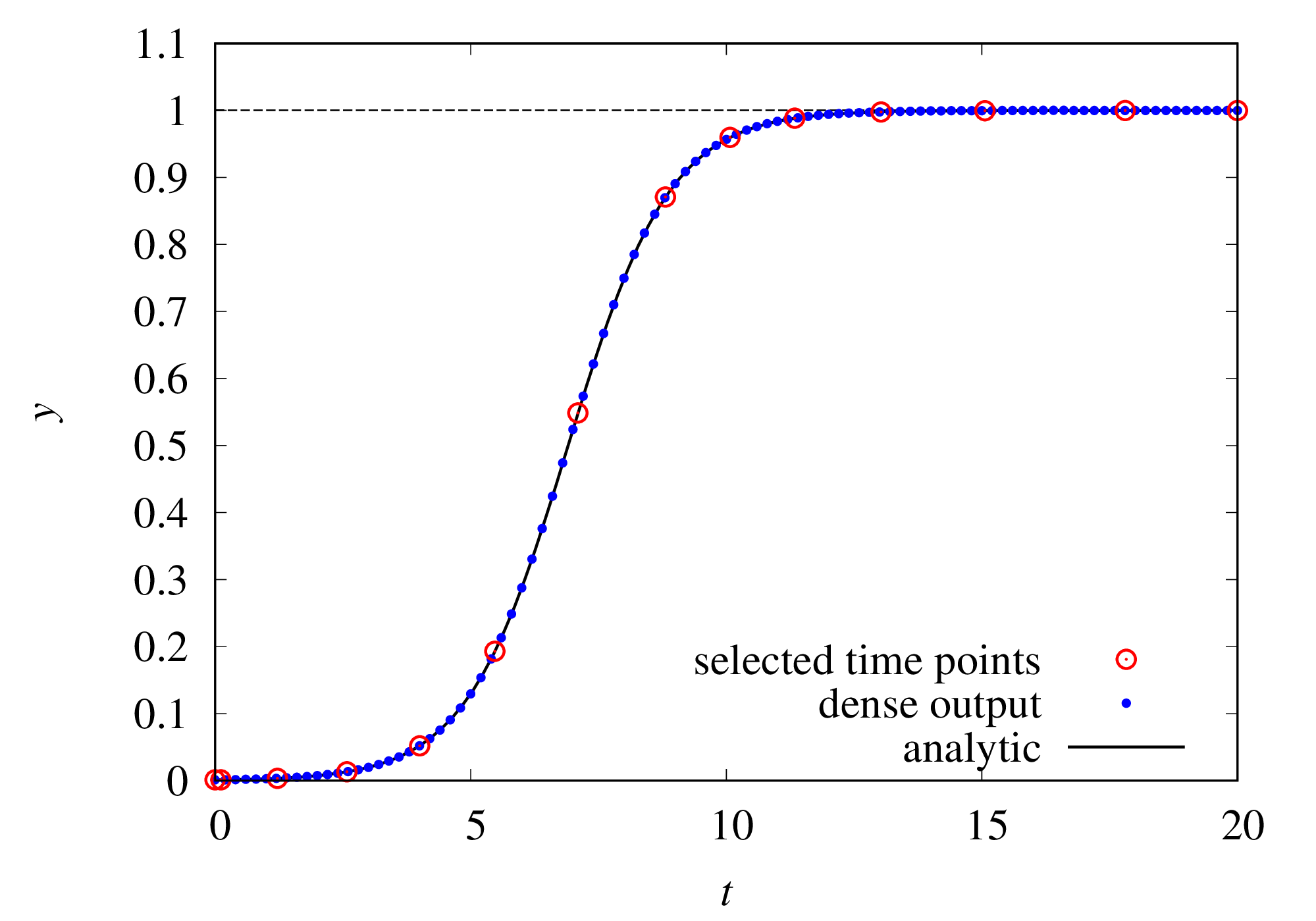
赤丸は自動的に選択された時刻における結果、青点は dense_output を使って細かく取った結果です。黒線が (2) 式の厳密解で、数値結果が正しいことが確認できます。赤丸はわずか14点しかありません。ソルバーが効率よく時間を進めていることが分かります。

4.2. 【例題】ロジスティック方程式¶

4.2.1. 方程式 ¶

方程式の解説 ¶

4.2.2. 実装 ¶

4.2.3. 結果 ¶

目次

前のトピックへ

次のトピックへ

4.2. 【例題】ロジスティック方程式¶

4.2.1. 方程式¶

方程式の解説¶

4.2.2. 実装¶

4.2.3. 結果¶

4.2.1. 方程式 ¶

方程式の解説 ¶

4.2.2. 実装 ¶

4.2.3. 結果 ¶