7.2. 【例題】デバイ模型の格子比熱

7.2.1. 数式

統計物理学で扱うデバイ模型（音波分散を考慮に入れた格子振動）の比熱を無次元化すると以下の積分で表されます：

(1)

ここで、 は温度をデバイ振動数 で無次元化した量 、 積分変数 は振動数 を のように無次元化した量です。

この積分は解析的に実行できないので、統計力学の教科書では低温極限 と高温極限 を考えて、積分を解析的に評価しています。数値積分を使って一般の温度における比熱の値を計算してみましょう。

7.2.2. 実装

ソースコード debye.py

数値積分の方法 で解説したように、被積分関数 を任意の点 で計算できる場合には、 scipy.integrate.quad 関数を使います。この関数の詳細は scipy.integrateの使い方 もしくは公式ドキュメントを参照してください。

まず、被積分関数を定義します。

def integrand(x):
    if x==0:
        return 0
    return x**4 / np.sinh(x/2.)**2

sinhの計算にはNumPyにある関数を使用します。NumPyで利用できる数学関数の一覧は Mathematical functions にあります。 のときに分母が0になってしまうので、場合分けをしています。より正確に実装するなら、 近傍でテイラー展開の式を使って計算します。

次にここで定義した関数を scipy.integrate.quad 関数に渡すことで数値積分を行います。

def specific_heat(t, verbose=False):
    if t==0:
        return 0
    y, err = integrate.quad(integrand, 0, 1./t)
    if verbose:
        print(f"integral : {y}")
        print(f"error    : {err}")
    return (3./4.) * t**3 * y

あとはこの関数を呼び出せば計算できます。 main関数を定義して、if __name__ == '__main__': からmain関数を呼び出すようにしておきます。

def main():
    t = 0.1
    c = specific_heat(t, verbose=True)
    print(f"T = {t}")
    print(f"c = {c}")

7.2.3. 実行結果

$ python debye.py
integral : 101.094670708
error    : 7.2900227173e-07
T = 0.1
c = 0.0758210030311

7.2.4. 温度変化

さて、数値積分が実行できるようになったので、 を変えて計算しましょう。先ほどのファイルdebye.pyはそのままにして置いておき、別のファイルを用意して新たにmain部分だけを書きます。

ソースコード debye_t.py

以下のようにインポートすることで、debye.pyの中で定義されたspecific_heat関数が使えるようになります：

from debye import specific_heat

このとき、debye.pyのスクリプトが一通り実行されますが、if __name__ == '__main__': 以下は無視されます。したがって、debye.pyにあるmain関数は実行されません。後は、 の値を変化させながら specific_heat 関数を繰り返し呼び出せば温度変化を計算できます。

def main():
    tmin = 0
    tmax = 2
    n = 201
    for t in np.linspace(tmin, tmax, n):
        c = specific_heat(t)
        print(f"{t:.4f} {c:.5e}")

t を tmin から tmax まで等間隔に分割するのに numpy.linspace 関数を使っています。 linspace はデフォルトで終点も含めるようになっているので、点の数を n=201 としてきりの良い間隔になるようにしています。

実行して得られた結果を図示すると以下のようになります。

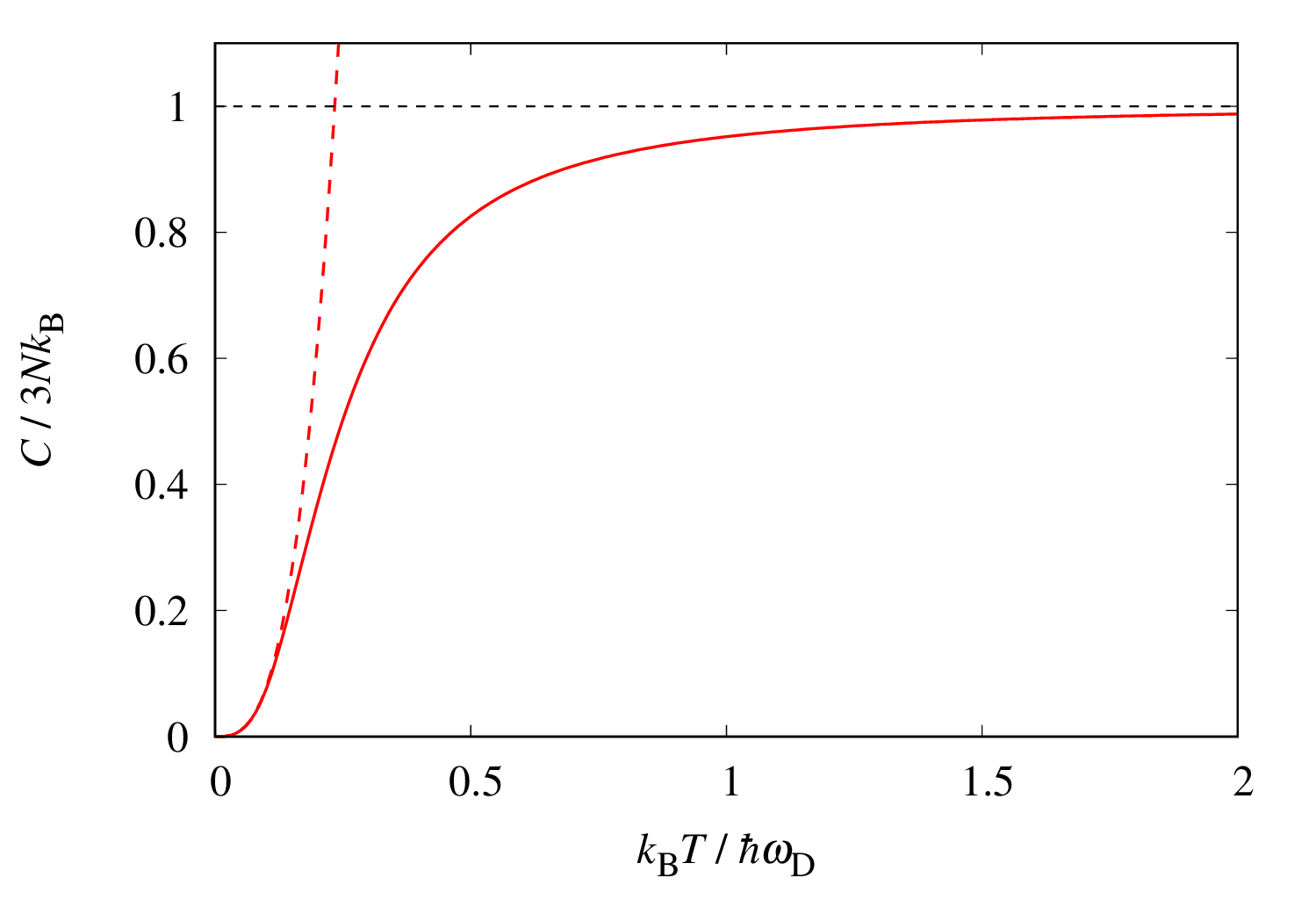
破線は低温における近似式 で、 においてよい近似になっていることが確認できます。