4.3. 【例題】ニュートン方程式

4.3.1. 方程式

ニュートン方程式を考えます。ここでは、重力に加えて、空気抵抗も考慮することにします。空気抵抗は速度に比例する逆向きの力として、F_\mathrm{resist}=-bv の形を仮定します。比例係数 b は物体の形や空気密度などに依存します。

物体の座標 x(t) に関する方程式は

(1)m\frac{d^2x(t)}{dt^2} &= F -b\frac{dx(t)}{dt}

と書けます。以下では、力 F は時間と座標に依らない定数とします。

連立1階微分方程式へ変形

ニュートン方程式は2階の微分方程式ですが、SciPyなど多くのライブラリは連立1階微分方程式 d\bm{y}(t)/dt = f(t, \bm{y}(t)) を解くように設計されています（常微分方程式の解法 を参照） 。そこで、ニュートン方程式を連立1階微分方程式の形に書き換えます。

速度 v=dx/dt を使うと、(1) 式は dv/dt = F/m - (b/m) v と表されます。したがって、座標と速度を合わせた2成分ベクトル \bm{X}(t)=(x(t), v(t)) を導入すると、(1) 式は

(2)\frac{d\bm{X}(t)}{dt} = \begin{pmatrix} 0 & 1 \\ 0 & -b/m \end{pmatrix} \bm{X}(t) + \begin{pmatrix} 0 \\ F/m \end{pmatrix}

の形の連立1階微分方程式となります。 この右辺をライブラリに与えて方程式を解きます。

2次元へ拡張

さて、1次元ではあまり面白くないので、2次元空間内の運動を解いて、軌道を図示することにします。水平右方向をx座標、鉛直上方向をy座標として、原点から、水平面との角度 \theta で球を飛ばす状況を考えます。空気抵抗がなければ、\theta=45^{\circ} の時に飛距離が最大になりますが、空気抵抗がある場合には、最適な角度は小さくなります。実際に球の軌道を描いて、確認してみましょう。

(2) 式を2次元に拡張すると、\bm{X}(t)=(x(t), v_x(t), y(t), v_y(t)) として

(3)\frac{d\bm{X}(t)}{dt} = \begin{pmatrix} 0 & 1 & 0 & 0 \\ 0 & -b/m & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & -b/m \end{pmatrix} \bm{X}(t) + \begin{pmatrix} 0 \\ 0 \\ 0 \\ -g \end{pmatrix}

となります。g は重力加速度です。この方程式を解いていきます。

4.3.2. 実装

ソースコード newton.py

まずは、方程式 (3) の右辺を作ります。

10def f_newton(t, X, m, g, b):
11    # X = [x, v_x, y, v_y]
12    dXdt = np.array([
13        X[1],              # dx/dt = v_x
14        -(b/m) * X[1],     # dv_x/dt = -(b/m) v_x
15        X[3],              # dy/dt = v_y
16        -(b/m) * X[3] - g  # dv_y/dt = -(b/m) v_y - g
17    ])
18    return dXdt

関数の形は f(t,y) と決まっているので、第1引数の t は使わないですが省略できません。第2引数 X が4成分ベクトル \bm{X} で、 3番目以降の引数 m, g, b はパラメーターです。この関数は、これら5個の引数を受け取り、(3) 式の右辺を計算して、4成分ベクトル d\bm{X}/dt を返します。

次に、方程式を解いて結果を返す関数を作ります。

21def solve_newton(eq_params, X0, t_range, n_t):
22    m, g, b = eq_params
23    t_start, t_end = t_range
24
25    # Solve ODE
26    sol = solve_ivp(f_newton, (t_start, t_end), X0, args=(m, g, b), dense_output=True)
27    print(sol.message)
28
29    # Get dense output for plot
30    t = np.linspace(t_start, t_end, n_t)
31    Xt = sol.sol(t)
32    assert Xt.shape == (4, n_t)
33
34    # x(t), v_x(t), y(t), v_y(t)
35    return Xt[0, :], Xt[1, :], Xt[2, :], Xt[3, :]

第1引数 eq_params は方程式のパラメーターをまとめたものです（関数の引数が多くなるのを避けるため）。eq_params は22行目で m, g, b に展開されます（unpackといいます）。第2引数 X0 は初期値です。第3引数 t_range は時刻の範囲で、第4引数 n_t が作図に使用する点の数です（方程式を解く際の時間刻みではありません）。

26行目：scipy.integrate.solve_ivp 関数を使って方程式を解きます（詳細は 常微分方程式の解法 を参照）。第1引数に先ほど作った関数 f_newton を与え、第2引数に初期時刻・終了時間、第3引数に初期条件を与えます。いま f_newton はパラメーターを3つ取る（3番目以降に引数が3つある）ように定義されているので、args にそれらの値を与えます。dense_output=True は作図用のデータを得るために指定しておく必要があります。

30～32行目：作図用のデータを取得します。まず、numpy.linspace で時刻の配列を作成し、この配列 t を、sol.sol(t) として先ほど得られた結果に与えると、各時刻での \bm{X}(t) が得られます。\bm{X}(t) が4成分なので、得られる結果 Xt は4 × n_t のNumPy配列です。32行目：assert 文で Xt のサイズを確認しています。もし、この等式が成り立っていない場合は、AssertionError エラーでプログラムが止まります。 assert文は、プログラムの間違いを早期に発見するためでもありますし、コードを読む人（自分も含む）へのメッセージという意味もあります。

35行目：最後に、x(t), v_x(t), y(t), v_y(t) の結果をそれぞれ1次元配列として返します。

さて、ここまで準備ができたら、パラメーターを与えて実際に方程式を解きます。

50def main():
51    # MKS units: m, kg, s
52    g = 9.8  # [m/s^2]
53    m = 0.1  # [kg]
54    b = 0.1  # [kg/s]
55
56    t_start = 0  # [s]
57    t_end = 5.0  # [s]
58    n_t = 101
59
60    # initial state
61    v0 = 100.0 / 3.6  # [m/s]
62    theta = 45 * (np.pi / 180)  # radian
63
64    # X0 = [x0, v0_x, y0, v0_y]
65    X0 = np.array([0, v0 * np.cos(theta), 0, v0 * np.sin(theta)])
66
67    # Solve Newton equation
68    # x(t), y(t)
69    xt, _, yt, _ = solve_newton(eq_params=(m, g, b), X0=X0, t_range=(t_start, t_end), n_t=n_t)

図の描画部分は除いています。

51～62行目：パラメーターをMKS単位系で指定しています。野球ボールを投げることを想定して、質量m=0.1kg、初速度v0=100km/h、角度theta=45°としています（人が投げる程度の速さです）。空気抵抗係数は直感的に決めることが難しいですが、ここではb=0.1kg/sとしています。逆に、結果を見て、飛距離からbを決めると考えた方が良いかもしれません。時刻0秒から5秒までを n_t=101 分割した結果、つまり0.05秒間隔のデータが得られます（繰り返しですが、これは微分方程式を解く際の時間刻み幅ではありません）。

65行目：初期条件を設定しています。

69行目：方程式を解いて、x(t) と y(t) を受け取ります。 2番目と4番目の戻り値（v_x(t) と v_y(t)）は今回は使わないので、アンダースコアで受け取っています。 慣例的に、使用しない戻り値はアンダースコアで受けることになっています。

4.3.3. 結果

スクリプトを実行すると、sol.message の出力が表示されます。微分方程式を解いた結果（ステータス）が文章として表示されます。

$ python3 newton.py
The solver successfully reached the end of the integration interval.

下図が結果です。空気抵抗のために横方向の速度が次第に遅くなり、最後は垂直に近い角度で地面に落下していることが分かります。

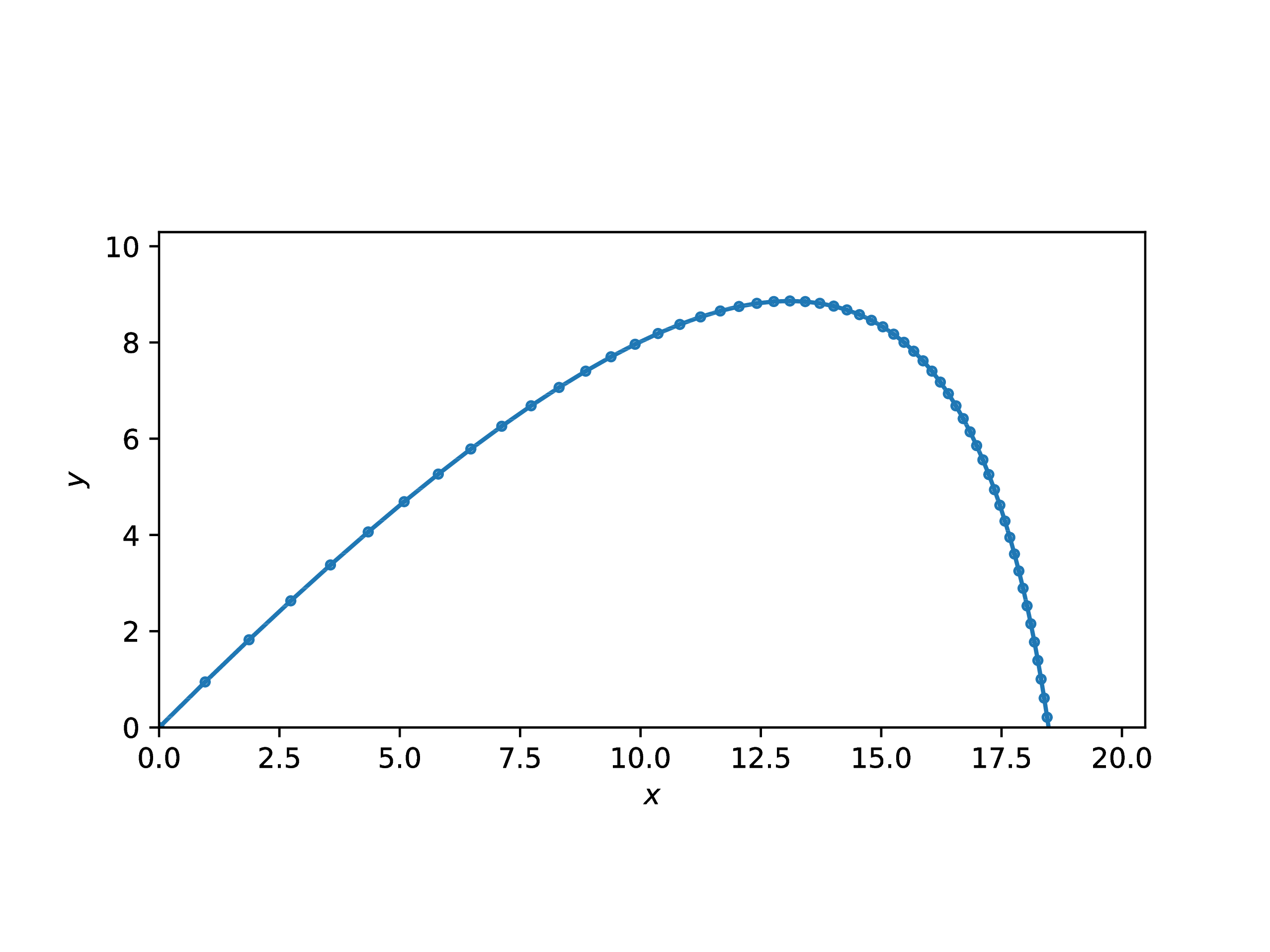
../_images/newton.png

注釈

図ではy>0のみを図示していますが、実際の軌道はy<0まで続いています。例えば、球がy=0に到達した時点で計算をストップしたい場合、あるいは、y=0で球が跳ね返るような軌道を計算したい場合には、solve_ivp 関数の events オプションを使って、y=0に到達する時刻を検出します。詳細は公式ドキュメント scipy.integrate.solve_ivp を参照してください。

4.3.4. 角度依存性

さて、角度を変えて計算をしてみましょう。 次のスクリプトファイルを、先ほどのスクリプトと同じ場所においてください。

ソースコード newton_angles.py

まずは、先ほどのファイルnewton.pyで定義した solve_newton 関数を使用するためにインポートします。

3from newton import solve_newton

角度を変えながら solve_newton 関数を繰り返し実行します。

21def main():
22    # MKS units: m, kg, s
23    g = 9.8  # [m/s^2]
24    m = 0.1  # [kg]
25    b = 0.1  # [kg/s]
26
27    t_start = 0  # [s]
28    t_end = 5.0  # [s]
29    n_t = 101
30
31    # initial state
32    v0 = 100.0 / 3.6  # [m/s]
33
34    # Results will be stored into a list as namedtuple
35    results = []
36    Result = namedtuple('Result', ['key', 'xt', 'yt'])
37
38    for theta_degree in range(5, 90, 5):
39        theta = theta_degree * (np.pi / 180)  # radian
40
41        # X0 = [x0, v0_x, y0, v0_y]
42        X0 = np.array([0, v0 * np.cos(theta), 0, v0 * np.sin(theta)])
43
44        # Solve Newton equation
45        # x(t), y(t)
46        xt, _, yt, _ = solve_newton(eq_params=(m, g, b), X0=X0, t_range=(t_start, t_end), n_t=n_t)
47
48        # Store result
49        results.append(Result(str(theta_degree), xt, yt))
50
51    plot(results)

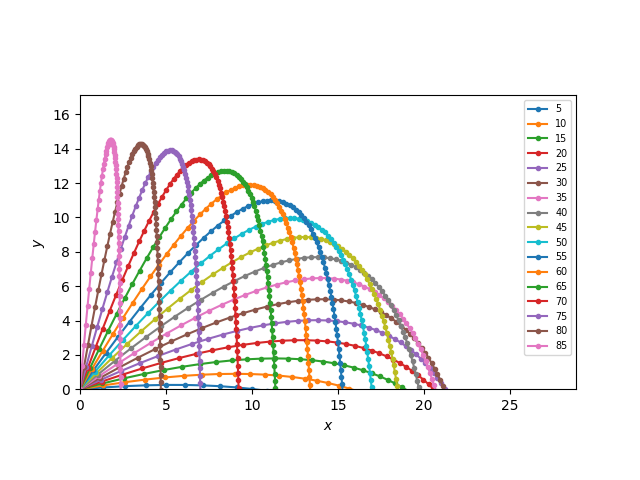
35行目：それぞれの角度における結果を保存するための空のリスト results を生成します。 36行目：\theta, x(t), y(t) をまとめて保存するために、collections.namedtuple を使って簡易クラス（C言語の構造体のようなもの）を定義しています。 38行目：角度を5°から85°まで5度間隔でforループで回して、それぞれニュートン方程式を解きます。 49行目：計算が終わるたびに、先ほど定義したnamedtupleを使ってデータをひとまとめにしてリスト results に追加します。

さて、計算結果を全て得たら、最後に図を作ります。

 7def plot(results):
 8    fig, ax = plt.subplots()
 9    for r in results:
10        ax.plot(r.xt, r.yt, marker='.', label=r.key)
11    ax.set_xlim(left=0)
12    ax.set_ylim(bottom=0)
13    ax.set_xlabel(r'$x$')
14    ax.set_ylabel(r'$y$')
15    ax.set_aspect('equal')  # plot x and y in an equal scale
16    ax.legend(fontsize='x-small')
17    # fig.show()
18    fig.savefig("newton_angles.png")

9行目：forループを回して、異なる角度の結果を順に取得します。 10行目：結果はnamedtupleで保存してあるので、r.xt や r.yt のような記法でデータにアクセスできます。このように表記が分かりやすくなるのがnamedtupleの特長です。通常のタプルを使用した場合には、r[0] や r[1] のようにデータにアクセスするので、r[0] や r[1] がどのデータに対応しているのか一目ではわからず、間違いが生じやすくなります。

実行して得られた図は以下の通りです。角度が約30°の時に飛距離が最大になっています。

../_images/newton_angles.png